=========================
n次元での距離と力
n次元での距離の算出方法と
n次元での、
その距離の増大に対する力の減衰についての式
ーーーーーーーーーーーーーーーーーーーーーーーーー
CopyRight Miyama. 2025 April
http://kazutomimiyama.sakura.ne.jp
KazukiKimijimaSub@gmail.com
=========================
これは、人工知能の基礎の一部にもなっている、多次
元空間での仮想重力についての考察:メモです。
せんだっての雑文のなかで思い出し、メモとして記し
てとおこうと思いました。
数学とは言語の一種であり、決して自然の博物学的な
詳細を記述するための体系ではありません。
いわば現実でない空間も、でっち上げればできてしま
うのが仮想という意味での言語空間とも言えます。
以下の論述も、n次元の空間というものがこの3次元
空間からの素朴な延長であるという課程に基づいて記述
してあるいわば楽観極まりない論議の一種である、とも
言えます。
素朴なユークリッド的な直線幾何が支配するn次元の
空間において、
・2点間の距離を算出する式、
・その次元における幾何に基づいた電磁気力や重力の
ような3次元における、逆二乗の法則のような、力の減
衰について、
単純な数式において素朴に考察します。
n次元に対する拡張は、素朴に楽天的なものです。
物理の最前線のトピックのダイジェストに考える限り、
現実の時空やそれに付随する一般宇宙論は、どうもこん
なものではないようです。あえて、そのことをここに付
記します。
ーーーーーーーーーーーーーーーーーーーーーーーーー
凡例表記、
Lは数学では小文字であらわされますが、
ワープロ上では、縦棒線になってしまうのであえて大
文字にしました。
Xd、Ydという表記は、
2点間の関係における、例えばx軸要素y軸要素のそ
れぞれの差分値であるために採用した表記です。
ただ以下の議論では、概念をわかりやすくするために、
始点の座標が、原点に等しいとする立場をとっています。
次の項、距離比における力減衰の式の説明では、この
ような利便を使えなかったのがやや歯がゆい経験ではあ
りました。
・2次元空間では、概念は比較的に楽です。
座標系が直交していますので、直角三角形に対するピ
タゴラスの定理がそのまま使えます。
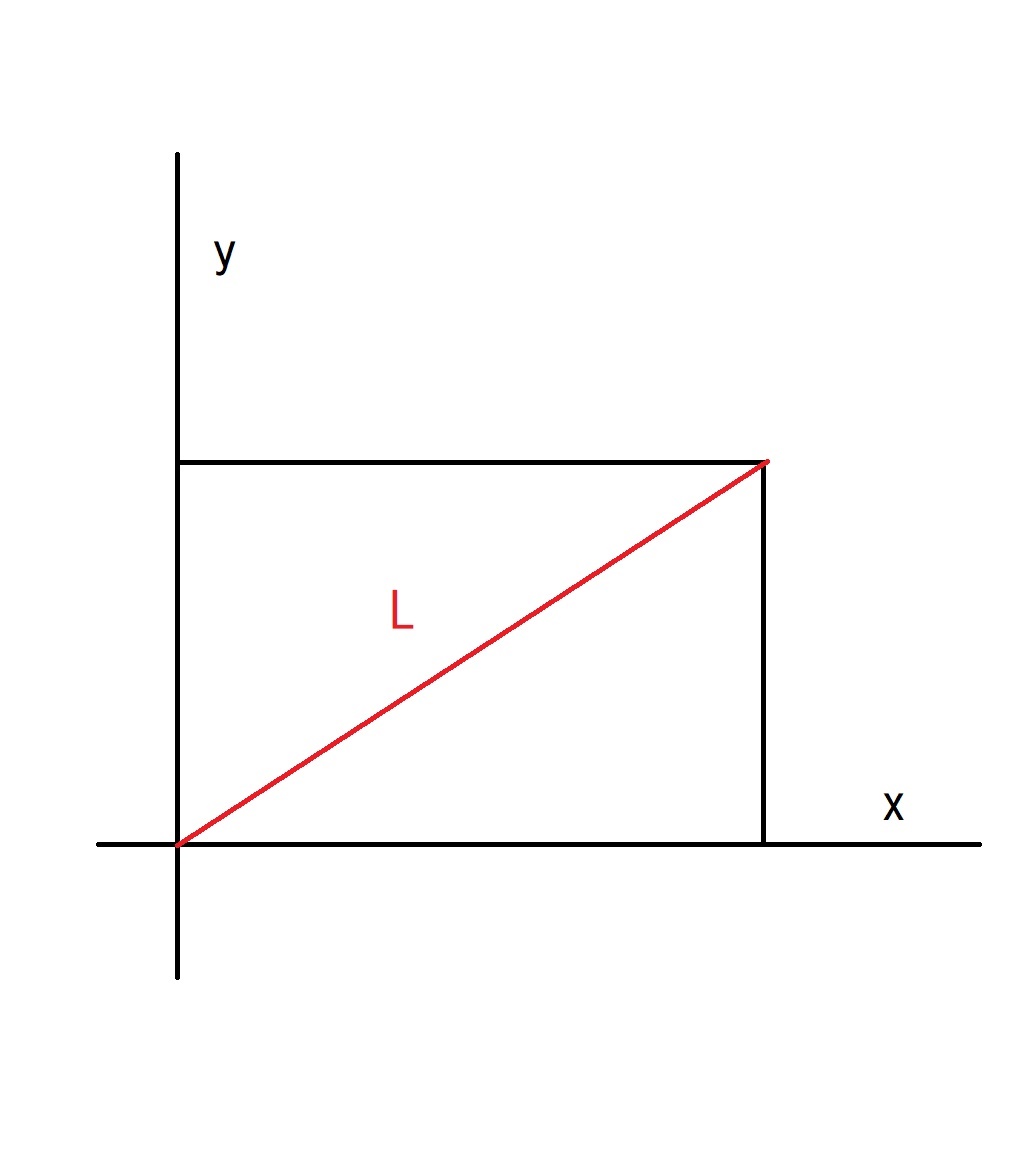 ------------
L = / Xd^2 + Yd^2
すなわち
L^2 = Xd^2 + Yd^2
でもあります。
------
・3次元では、やや複雑になります。
補助線としてのLtmpという長さを導入すれば、これも
一般式を導くことができます。
------------
L = / Xd^2 + Yd^2
すなわち
L^2 = Xd^2 + Yd^2
でもあります。
------
・3次元では、やや複雑になります。
補助線としてのLtmpという長さを導入すれば、これも
一般式を導くことができます。
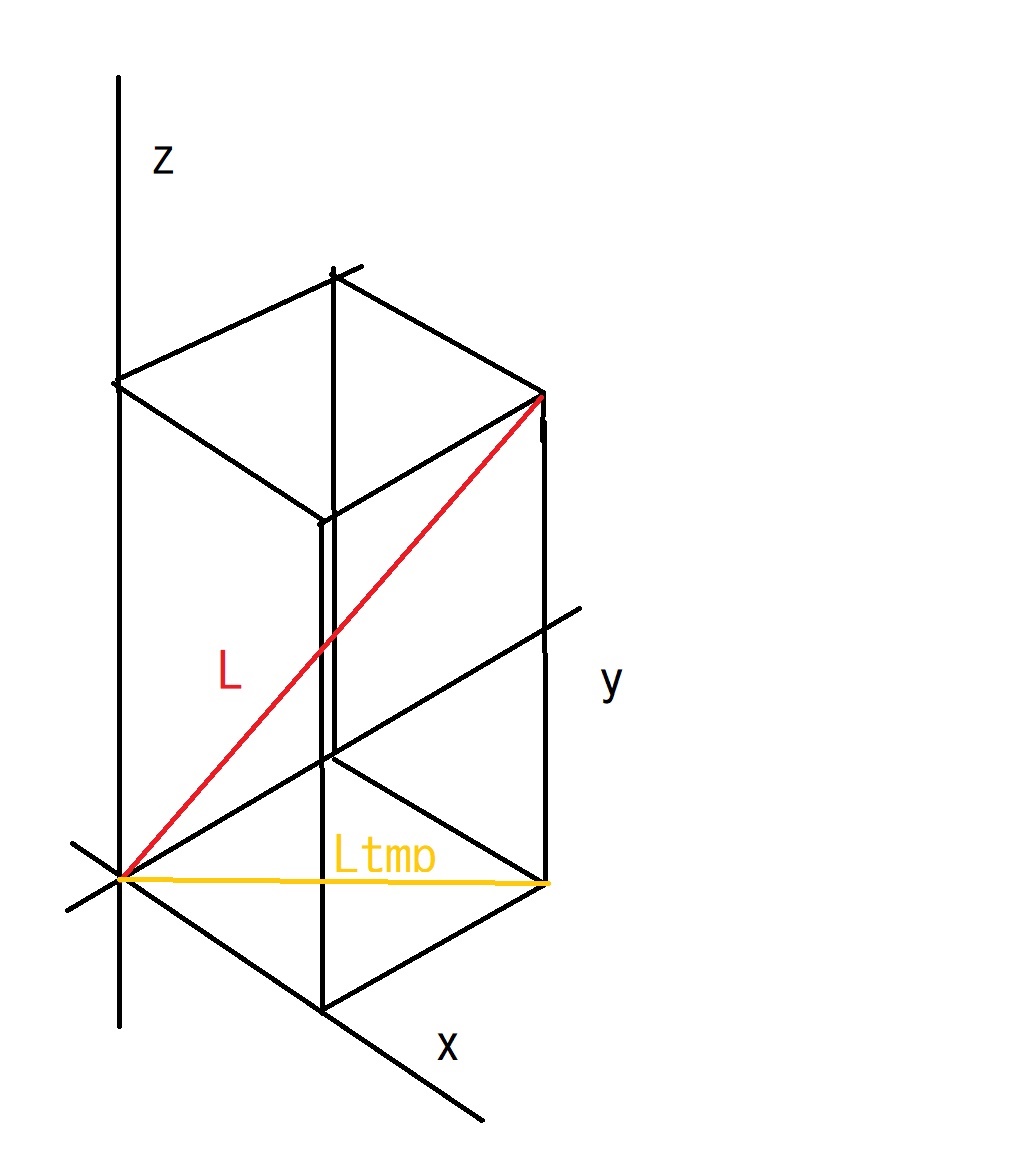 Ltmp^2 = Xd^2 + Yd^2
L^2 = Zd^2 + Ltmp^2
= Xd^2 + Yd^2 + Zd^2
-----
・ここから楽観的な拡張をn次元に対して行います。
2次元から3次元に対してZ軸の項が素朴に追加され
たことを、多次元においても一般的に成り立つと強引に
仮定すると、以下の一般式を導くことができます。
L^2 = Xd^2 + Yd^2 + Zd^2 + ... + Ad^2
:A is Any Added Demention
Aは任意の多次元目の座標軸です。
これを数式的に処理しやすいように、配列的に表記す
ると、
n次元空間における、2点間の距離の(二乗)は以下
のように表現できます。
L^2 = D(0)d^2 + D(1)d^2 + D(2)^2 + ... + D(n-1)d^2
n-1
=sigma D(k)d^2
k=0
Dは次元:ディメンションの略です。
-----
・空間における力の減衰に対しての考察
始点の原点(力源)からの距離をDistance1、
終点の力源からの距離を同じく Distance2とします。
結果選出されるそれぞれの力をDyn1Dyn2とします。
議論をわかりやすくするために、力源と始点と終点は
同一直線状にあるとします。
・2次元の場合
Ltmp^2 = Xd^2 + Yd^2
L^2 = Zd^2 + Ltmp^2
= Xd^2 + Yd^2 + Zd^2
-----
・ここから楽観的な拡張をn次元に対して行います。
2次元から3次元に対してZ軸の項が素朴に追加され
たことを、多次元においても一般的に成り立つと強引に
仮定すると、以下の一般式を導くことができます。
L^2 = Xd^2 + Yd^2 + Zd^2 + ... + Ad^2
:A is Any Added Demention
Aは任意の多次元目の座標軸です。
これを数式的に処理しやすいように、配列的に表記す
ると、
n次元空間における、2点間の距離の(二乗)は以下
のように表現できます。
L^2 = D(0)d^2 + D(1)d^2 + D(2)^2 + ... + D(n-1)d^2
n-1
=sigma D(k)d^2
k=0
Dは次元:ディメンションの略です。
-----
・空間における力の減衰に対しての考察
始点の原点(力源)からの距離をDistance1、
終点の力源からの距離を同じく Distance2とします。
結果選出されるそれぞれの力をDyn1Dyn2とします。
議論をわかりやすくするために、力源と始点と終点は
同一直線状にあるとします。
・2次元の場合
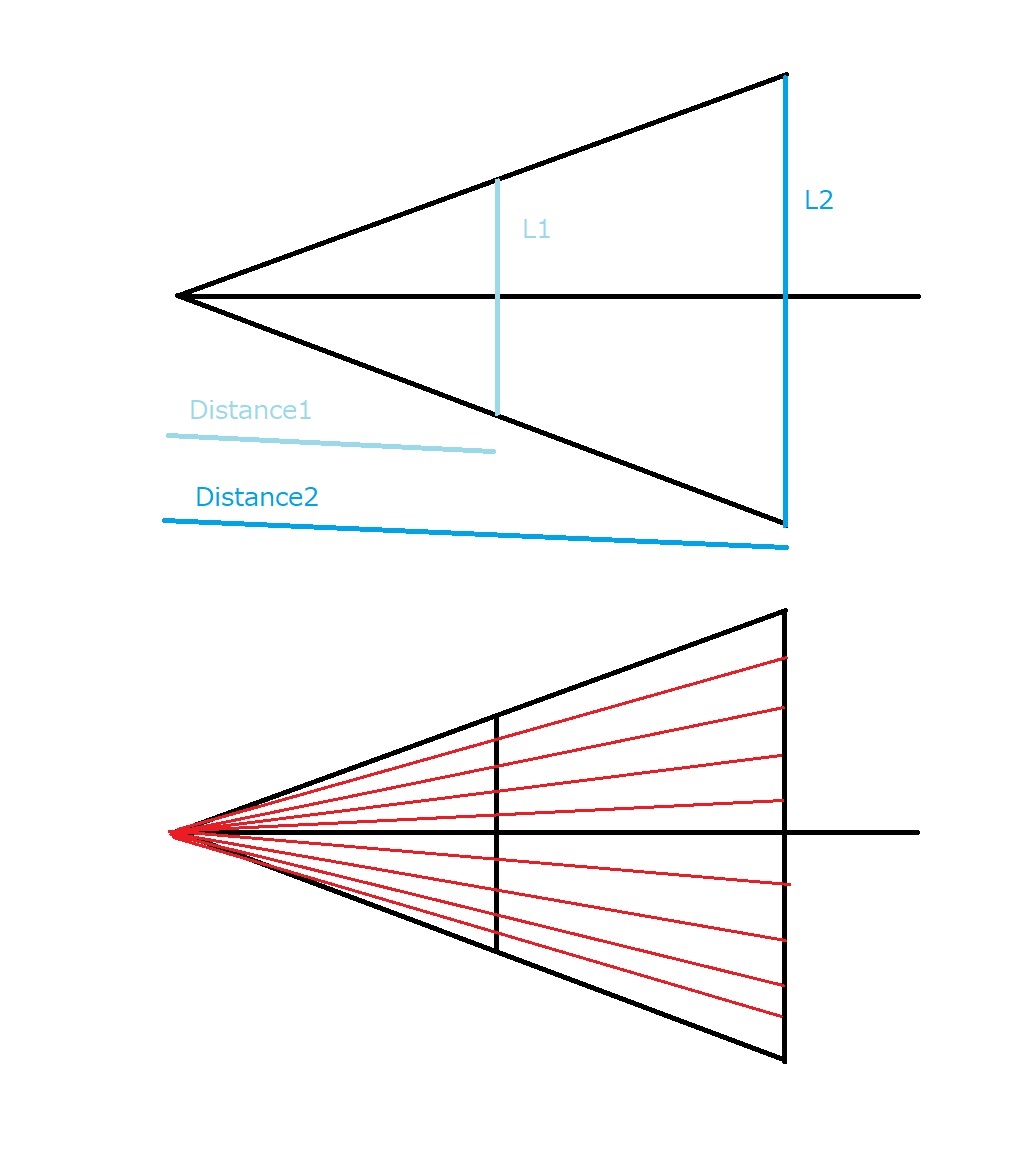 力線が作用する(微小)被作用直行線をL1L2とします。
2次元幾何的に、始点終点の距離の比と、作用を受け
る直行線の比率は同一です。
力の強弱は仮想的な力線がどれだけ被作用線に交差す
るかという密度の概念で決まりますから、2次元では力
の強弱は距離の比に単純に反比例する、という式によっ
て表現することができます。
Distance1:Distance2 = L1:L2 = 1:2
L1 Distance1 1
Dyn2 = Dyn1*---- = Dyn1*--------- = Dyn1*---
L2 Distance2 2
: Dyn1*Distance1 = Dyn2*Distance2 = const
受ける力は、距離に反比例します。
-----
・3次元の場合
力線が作用する(微小)被作用直行線をL1L2とします。
2次元幾何的に、始点終点の距離の比と、作用を受け
る直行線の比率は同一です。
力の強弱は仮想的な力線がどれだけ被作用線に交差す
るかという密度の概念で決まりますから、2次元では力
の強弱は距離の比に単純に反比例する、という式によっ
て表現することができます。
Distance1:Distance2 = L1:L2 = 1:2
L1 Distance1 1
Dyn2 = Dyn1*---- = Dyn1*--------- = Dyn1*---
L2 Distance2 2
: Dyn1*Distance1 = Dyn2*Distance2 = const
受ける力は、距離に反比例します。
-----
・3次元の場合
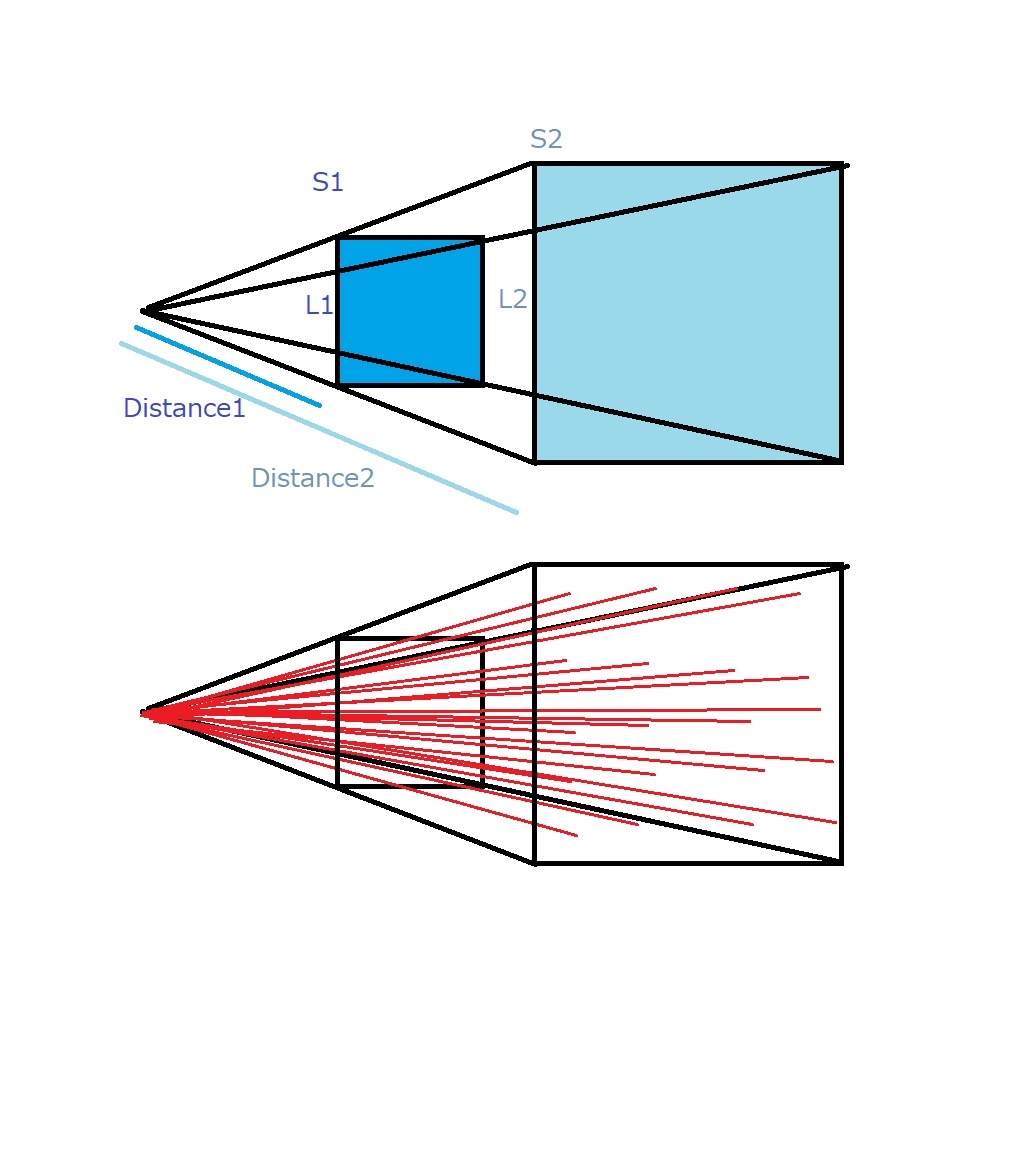 力線が作用するのは、線分でなく単位面積になります。
ここまで状況差分を一般化すると、2次元で力線が
作用するのは、単位微線分:1次元、
3次元では、単位微細面積:2次元、
ということになります。
被作用面積をS1S2とすると、
面積比は線分比の二乗になりますから、
力線密度をこの距離比=線分比の二乗で分け合うこと
になり、以下、
Distance1:Distance2 = L1:L2 = 1:2
S1 (Distance1)^2 1
Dyn2 = Dyn1*---- = Dyn1*(---------) = Dyn1*---
S2 (Distance2) 4
: Dyn1*(Distance1)^2 = Dyn2*(Distance2)^2
それぞれの点において、受ける力と距離の二乗の積は
一定、
つまり二次元の世界よりは、離れれば離れるほど受け
る力は弱くなります。
・n次元へ拡張
n次元でも、力線を受ける当該微小単位は
n-1次元の超断面をもつとすると、2,3次元の力の結
論は、次の式に一般化されます。
Dyn1*(Distance1)^(n-1) = Dyn2*(Distance2)^(n-1)
ここで式の概念をわかりやすくするために変形します。
(Distance1)^(n-1) (Distance1)^(n-1) (Distance2)^(-(n-1))
Dyn1*----------------- = Dyn2= Dyn1*(---------) = Dyn1*(---------)
(Distance2)^(n-1) (Distance2) (Distance1)
この式を式*とします。
Distance1、Dyn1の点を、1単位とし、
Distance2、Dyn2の点を、任意の一般点とすると、
その点の距離と受ける力は
DistanceRate、DynRateとなります。
Dyn2 Distance2
DynRate = ----- 式*1 , DistanceRate = --------- 式*2
Dyn1 Distance1
式*2を式*に代入し、
Dyn2 = Dyn1*DistanceRate^(-(n-1))
またこの式の両辺をDyn1で割り、
Dyn2 1
------ = DistanceRate^(-(n-1)) = ------------------
Dyn1 DistanceRate^(n-1)
つまりこれは、
= DynRate
改めて清書すると
1
DynRate = ------------------
DistanceRate^(n-1)
空間次元が上がるほど、遠方で受ける力は
急速に弱くなるようです。
-----
・n次元の任意点
P(D(0)d, D(1)d, D(2)d, ... D(n-1)d)
厳密には始点を原点=力源に置いていますので、差分
を表すdの文字は意味がありません。
差分の意味dを任意点pの意味に書き換えます。
P(D(0)p, D(1)p, D(2)p, ... D(n-1)p)
における、力源=原点を始点とする
長さ1の任意ベクトルが差す任意の点に置ける
力を1とした場合の受ける力を表す式は、
始点が原点であれば、LとDistanceRateは同義ですから、
L = Distantrate
L^2 = D(0)p^2 + D(1)p^2 + D(2)p^2 + ... + D(n-1)p^2
L = ( D(0)p^2 + D(1)p^2 + D(2)p^2 + ... + D(n-1)p^2 )^(1/2)
1 1
DynRate = -------- = --------------------------------------------------------
L^(n-1) (n-1)
(---)
( D(0)p^2 + D(1)p^2 + D(2)p^2 + ... + D(n-1)p^2 )^( 2 )
となります。形式的には。
※これは、太陽系のような中心にほぼ絶対的に重い重
力力点が存在するような系での概念です。
キャベンディシュの実験によってもたらさられた見解
は、地球と分銅の関係において、驚くべきことに分銅に
も引力を発生する力が存在していることです:万有引力。
意味空間のアナロジーの手本となった、星団星雲内の
個々の恒星の相互作用は、それぞれの恒星ごとに重力の
相互作用の積算が存在することであり、
ある星Aがある星Bに対して及ぼす重力の強さを算出す
るばあい、
それぞれの星が距離Lだけ離れている場合は、
その演算においては、Xd、Yd、Zdという距離差分によ
って導き出された力比:DyneRateにその星Aの質量GAを
掛けた値になります。
具体的には、現実宇宙の近似として、
星1000個の恒星星団の場合、ある任意の星A(k)
に対して、
残り1000ー1=999個の星がそれぞれこれらの
差分演算からくる距離と個々の星の重力の積を演算1単
位とし、
それの999個分の重力影響の積算をもって、
それを単位時間ごとの加速度に変換し、
はじめてその任意の星A(k)の微小ステップ移動が算出
されるのです。
また、その任意の星A(k)も、計算ループの別のフェー
ズでは、
また別の星A(kdash)に影響を及ぼす重力源として、作
用に参加するのです。
・・・人間の考えることはそんなに特別なことではな
いはずですから、人工知能の単語空間における意味演算
もまたほとんどおなじプロセスをたどっているはずと推
測はしますが、
ただこの総当たり式のシミュレーションはおそろしく
べらぼうな演算量を必要とします。
3次元空間の星1000個の星団での演算は、
それぞれの星一つについてののこり999個の恒星の
重力影響の積算演算を、
全1000個の星ごとに行ってはじめて1ステップの
計算が終了するのです。
つまり、およそ
1000^2=10^(3+2)=10^5=10万演算
それが、計算精度を上げるためには、1ステップをで
きるだけ微細な時間単位を取らなければならないので、
なかなか演算が進捗しません。
星雲のシミュレーションも、人工知能も、
想像を絶する計算力を必要としますので、
このようなことが可能となったのは、やはりごく最近
になってからだ、ということはできるでしょう。
参考経験:多体問題999:思い切り手前味噌。
たしかソースコードはつけていたはずですので興味が
あるならどうぞ。
*
少し随想。
・力の作用が弱い高次元空間
素朴なこの数式を扱っておもったのは、高次元の空間
とは、ちょっと離れただけで重力などがほとんど作用し
なくなっている空間だということがわかります。
原子は電磁気力による電子の軌道、天体は重力による
惑星系や衛星の軌道、
高次元とはつまりこのようなものが存在しにくい空間
だとも考えられます。
ある程度高い次元の空間とは、素粒子がただスープの
ようにただようだけの、ほとんど事象がなにも起こらな
い空間だということも言えます。
そのような記述をどこかで読んだ記憶があります。
日経サイエンスだとは思いますが、
弱い人間原理に照らせば、この宇宙が3次元空間なの
は、ほかの高い次元では、生命を生むだけの物質の相互
作用がほとんど起きないからだ、と帰納することができ
るのかもしれません。
また2次元以下の宇宙では、影響力が逆に固くつぶれ
てしまって、窒息がごとくにこれも何も起きにくい世界
なのかもしれません。
どういう数学的背景なのかは多分筆者には理解できな
いと思いますが、この宇宙はもともと11次元であり、
のこりの次元は素粒子レベルの泡となってまるまってい
て、日常的な感覚では知覚できないからだという説もあ
ります。
そうだとするのならば、もともと多次元宇宙として始
まったこの宇宙が、何の因果か、それこそ事象現象の十
分な成立を優先させたがために、変形を進化というのは
微妙ですが、すくなくとも変化したともいえるのでしょ
うか?
・グルーオンについて
強い力というものは、距離がどこまで伸びてもその力
は一定だ、と核物理の入門書にはかいてあります。
素朴な感覚として、3次元空間にそんな力は存在しな
いはずです。
これも、たぶんどこかで読んだ記事だと思いますが、
強い力というものは素朴な意味でのこの宇宙空間の力で
はなく、相転移するまえの古い宇宙空間独特の力であり、
いわゆる核子、重粒子:ハドロンとは、
その相転移するまえの古い宇宙空間が断片化されて、
あたかも濡れた化繊のシャツが肌に張り付くときに、微
小な空気が閉じ込められて、線状の微細な個々のしわに
なるように、
現在の広大な宇宙空間に、閉じ込められた状態だ、
とするものです。
ハドロンの内側、
別の空間の別種の力であれば、それがこの新しい世代
の空間にもれでてこないのは道理で、
もし核子が高エネルギーをあたえられて、縁日屋台の
ひも風船のように引き延ばされた場合は、
その力学力線の断面積はどこも一定ですので、
よっていくらはなれても、力の強さはかわらない、
ということになります。
これは、思考としては、電磁力と弱い力が分離する前
の電核力と重力しかなかった時代、
もし宇宙が十分な大きさを持っていれば、その力は逆
2乗の法則に従って伝播していたとも考えられるのかも
しれません。
筆者は高等数学が全く分からないので、数式的にこれ
を理解することができません。
そのころの宇宙が、プランク単位程度の大きさしかな
ければその概念もまた危ういものではありますが。
・重力について
これもまた日経サイエンスのコラムだったと想います。
重力は本当は力ではないのではないか、という
疑念説があります。
別の物理的な機構が裏で働いている作用をあたかもそ
れが力であるように錯覚是認している、
と考えた方が、
論理の上では気が楽になる、
という主張です。
散文的な概念としては筆者はこちらに組したい気がし
ます。
重力をほかの3つの力とおなじものだと仮定して理論
をすすめると、概念的に無理をしなければそれがなりた
たない、といわれるからでもあります。
よく紹介されていた理論として、この世界とは別の存
在の宇宙があって、その宇宙が超次元的に「ちょっかい」
を出しているがゆえに、重力の事象が発生している、と
いうものがあります。
筆者はその話を読んだとき、因果律的にまったく没干
渉であるからこそ、宇宙が別々に存在している理由にな
っているんではないのかと素朴におもったものです。
つまり、この宇宙の事象を説明するのに、常時並行し
て同じような宇宙が存在することが必要なのだという概
念は、数式的要請なのかもしれませんが、あまり考えに
くいものです。
これならばワームホールや孫宇宙の生成という概念の
方がまだわかりやすい構想ではあります。
重力の異常な特徴として、
・+ーという意味での負の符号がない
・ほかの3つの力に比べてそのちからが極端に弱すぎる
その力の比とは、乱暴に言ってしまえば、素粒子と天
体の半径比と言い換えてもいいでしょう。べらぼうな累
乗の値になります。
重力はあるいは時空の性質の一側面なのではないかと
いう気がします。
空間構造の基本理解として、
騾馬電子、あるいはヒッグス粒子という表現がされて
いますが、それが概念的に正しいのかはよくわかりませ
ん。
それらの粒子がべったりと充填しているのが時空だと
説明されていますが、
もし粒子が広義のスピンをもった存在だとすれば、
粒子がべったりと充填された構造というのは、
スピンが部分的にほどけて、金網のようにあみあげら
れた状態が一見静的にみえる宇宙の真空の状態だとみる
ことができます。
この宇宙:真空での粒子の運動というものは、
まずその「泡」の渦巻きのむきが、小さな台風のよう
に逆むきになり、
またその移動とはその泡が、
金網を進行方向に部分的にほどき、
また後方を本来の金網の順法通りの網目にもどし結び
ながら、
金網の網目を、じゃーっと流れていく姿に近いのかも
しれません。
このような時空と粒子がどのように、一見重力のよう
にみえる現象を演出するのか、まったくもってわかりま
せんが、
一つには相対論の挙措が一つのヒントにはなるのかも
しれません。
すなわち
・巨視的には、質量が多く集積すると時空がゆがむ
・ゆがんだ時空は重力という力を及ぼすように見える
このふたつが同じものかどうかは筆者にはよくわかり
ません。
-----
・おまけ(いたずら)
天体の立体図を表現する時に使った概念を披露します。
XYZ軸が、ディスプレイ画面にたがいに60度の角
度で交わっている場合は、3次元の座標を2次元に以下
のように変換すれば俯瞰図を投影することができます。
DispX = Z*cos(0) + Y*cos(+30) + X*cos(-30)
DispY = Z*sin(0) + Y*sin(+30) + X*sin(-30)
Z軸が先頭に立っているのは一般化のためです。
カッコ内の角度も、配列符号的に管理することができ、
0 = 90 - 0*60
+30 = 90 - 1*60
-30 = 90 - 2*60
Z=D(0)、X=D(1)、Y=D(2) とおくと
3-1
DispX or Y = sigma D(k)*cos or sin(90 - k*60)
k=0
と積算記号を使えば一般化できます。
ラジアンで表現すると、
paiは円周率
90 = pai/4, 60 = 2pai/3 ですから
3-1 pai 2pai
DispX or Y = sigma D(k)*cos or sin(--- - ----)
k=0 4 3-1
です。
これをまた、多次元拡張をすると、
n-1 pai 2pai
DispX= sigma D(k) * cos( --- - ----)
k=0 4 n-1
n-1 pai 2pai
DispY= sigma D(k) * sin( --- - ----)
k=0 4 n-1
となり、多次元空間の点をディスプレイに投影できる
ことになります。
たとえばn=4とすると4次元空間の点を投影できます。
この場合は、右半分の象限がディスプレイ上は45度
で交わる4本の座標線で表現されます。
※注意
古来、風景画家は遠景の奥行きを出すことに苦労をし
てきました。3次元を2次元に投影することがもともと
幾何学的に無理があるからです。
人工建築のように単位当たりの区画の長さが一定なも
のであれば、単位長さを距離の反比例にすれば表現は可
能ですが、
自然風景になるともうおてあげです。
かすみの濃度が距離の関数であるということを、無理
に退ければ、空気遠近法は幾何ではありません。
それと同様に4次元以上の幾何体を2次元ディスプレ
イに投影するのがなにか意味があるかどうかはまったく
わかりません。
4次元形式のヤコビの楕円体を2次元ディスプレイに
投影しても、あたまがウニになるだけのような気もしま
すが。
=========================
ファイルの終わり
=========================
力線が作用するのは、線分でなく単位面積になります。
ここまで状況差分を一般化すると、2次元で力線が
作用するのは、単位微線分:1次元、
3次元では、単位微細面積:2次元、
ということになります。
被作用面積をS1S2とすると、
面積比は線分比の二乗になりますから、
力線密度をこの距離比=線分比の二乗で分け合うこと
になり、以下、
Distance1:Distance2 = L1:L2 = 1:2
S1 (Distance1)^2 1
Dyn2 = Dyn1*---- = Dyn1*(---------) = Dyn1*---
S2 (Distance2) 4
: Dyn1*(Distance1)^2 = Dyn2*(Distance2)^2
それぞれの点において、受ける力と距離の二乗の積は
一定、
つまり二次元の世界よりは、離れれば離れるほど受け
る力は弱くなります。
・n次元へ拡張
n次元でも、力線を受ける当該微小単位は
n-1次元の超断面をもつとすると、2,3次元の力の結
論は、次の式に一般化されます。
Dyn1*(Distance1)^(n-1) = Dyn2*(Distance2)^(n-1)
ここで式の概念をわかりやすくするために変形します。
(Distance1)^(n-1) (Distance1)^(n-1) (Distance2)^(-(n-1))
Dyn1*----------------- = Dyn2= Dyn1*(---------) = Dyn1*(---------)
(Distance2)^(n-1) (Distance2) (Distance1)
この式を式*とします。
Distance1、Dyn1の点を、1単位とし、
Distance2、Dyn2の点を、任意の一般点とすると、
その点の距離と受ける力は
DistanceRate、DynRateとなります。
Dyn2 Distance2
DynRate = ----- 式*1 , DistanceRate = --------- 式*2
Dyn1 Distance1
式*2を式*に代入し、
Dyn2 = Dyn1*DistanceRate^(-(n-1))
またこの式の両辺をDyn1で割り、
Dyn2 1
------ = DistanceRate^(-(n-1)) = ------------------
Dyn1 DistanceRate^(n-1)
つまりこれは、
= DynRate
改めて清書すると
1
DynRate = ------------------
DistanceRate^(n-1)
空間次元が上がるほど、遠方で受ける力は
急速に弱くなるようです。
-----
・n次元の任意点
P(D(0)d, D(1)d, D(2)d, ... D(n-1)d)
厳密には始点を原点=力源に置いていますので、差分
を表すdの文字は意味がありません。
差分の意味dを任意点pの意味に書き換えます。
P(D(0)p, D(1)p, D(2)p, ... D(n-1)p)
における、力源=原点を始点とする
長さ1の任意ベクトルが差す任意の点に置ける
力を1とした場合の受ける力を表す式は、
始点が原点であれば、LとDistanceRateは同義ですから、
L = Distantrate
L^2 = D(0)p^2 + D(1)p^2 + D(2)p^2 + ... + D(n-1)p^2
L = ( D(0)p^2 + D(1)p^2 + D(2)p^2 + ... + D(n-1)p^2 )^(1/2)
1 1
DynRate = -------- = --------------------------------------------------------
L^(n-1) (n-1)
(---)
( D(0)p^2 + D(1)p^2 + D(2)p^2 + ... + D(n-1)p^2 )^( 2 )
となります。形式的には。
※これは、太陽系のような中心にほぼ絶対的に重い重
力力点が存在するような系での概念です。
キャベンディシュの実験によってもたらさられた見解
は、地球と分銅の関係において、驚くべきことに分銅に
も引力を発生する力が存在していることです:万有引力。
意味空間のアナロジーの手本となった、星団星雲内の
個々の恒星の相互作用は、それぞれの恒星ごとに重力の
相互作用の積算が存在することであり、
ある星Aがある星Bに対して及ぼす重力の強さを算出す
るばあい、
それぞれの星が距離Lだけ離れている場合は、
その演算においては、Xd、Yd、Zdという距離差分によ
って導き出された力比:DyneRateにその星Aの質量GAを
掛けた値になります。
具体的には、現実宇宙の近似として、
星1000個の恒星星団の場合、ある任意の星A(k)
に対して、
残り1000ー1=999個の星がそれぞれこれらの
差分演算からくる距離と個々の星の重力の積を演算1単
位とし、
それの999個分の重力影響の積算をもって、
それを単位時間ごとの加速度に変換し、
はじめてその任意の星A(k)の微小ステップ移動が算出
されるのです。
また、その任意の星A(k)も、計算ループの別のフェー
ズでは、
また別の星A(kdash)に影響を及ぼす重力源として、作
用に参加するのです。
・・・人間の考えることはそんなに特別なことではな
いはずですから、人工知能の単語空間における意味演算
もまたほとんどおなじプロセスをたどっているはずと推
測はしますが、
ただこの総当たり式のシミュレーションはおそろしく
べらぼうな演算量を必要とします。
3次元空間の星1000個の星団での演算は、
それぞれの星一つについてののこり999個の恒星の
重力影響の積算演算を、
全1000個の星ごとに行ってはじめて1ステップの
計算が終了するのです。
つまり、およそ
1000^2=10^(3+2)=10^5=10万演算
それが、計算精度を上げるためには、1ステップをで
きるだけ微細な時間単位を取らなければならないので、
なかなか演算が進捗しません。
星雲のシミュレーションも、人工知能も、
想像を絶する計算力を必要としますので、
このようなことが可能となったのは、やはりごく最近
になってからだ、ということはできるでしょう。
参考経験:多体問題999:思い切り手前味噌。
たしかソースコードはつけていたはずですので興味が
あるならどうぞ。
*
少し随想。
・力の作用が弱い高次元空間
素朴なこの数式を扱っておもったのは、高次元の空間
とは、ちょっと離れただけで重力などがほとんど作用し
なくなっている空間だということがわかります。
原子は電磁気力による電子の軌道、天体は重力による
惑星系や衛星の軌道、
高次元とはつまりこのようなものが存在しにくい空間
だとも考えられます。
ある程度高い次元の空間とは、素粒子がただスープの
ようにただようだけの、ほとんど事象がなにも起こらな
い空間だということも言えます。
そのような記述をどこかで読んだ記憶があります。
日経サイエンスだとは思いますが、
弱い人間原理に照らせば、この宇宙が3次元空間なの
は、ほかの高い次元では、生命を生むだけの物質の相互
作用がほとんど起きないからだ、と帰納することができ
るのかもしれません。
また2次元以下の宇宙では、影響力が逆に固くつぶれ
てしまって、窒息がごとくにこれも何も起きにくい世界
なのかもしれません。
どういう数学的背景なのかは多分筆者には理解できな
いと思いますが、この宇宙はもともと11次元であり、
のこりの次元は素粒子レベルの泡となってまるまってい
て、日常的な感覚では知覚できないからだという説もあ
ります。
そうだとするのならば、もともと多次元宇宙として始
まったこの宇宙が、何の因果か、それこそ事象現象の十
分な成立を優先させたがために、変形を進化というのは
微妙ですが、すくなくとも変化したともいえるのでしょ
うか?
・グルーオンについて
強い力というものは、距離がどこまで伸びてもその力
は一定だ、と核物理の入門書にはかいてあります。
素朴な感覚として、3次元空間にそんな力は存在しな
いはずです。
これも、たぶんどこかで読んだ記事だと思いますが、
強い力というものは素朴な意味でのこの宇宙空間の力で
はなく、相転移するまえの古い宇宙空間独特の力であり、
いわゆる核子、重粒子:ハドロンとは、
その相転移するまえの古い宇宙空間が断片化されて、
あたかも濡れた化繊のシャツが肌に張り付くときに、微
小な空気が閉じ込められて、線状の微細な個々のしわに
なるように、
現在の広大な宇宙空間に、閉じ込められた状態だ、
とするものです。
ハドロンの内側、
別の空間の別種の力であれば、それがこの新しい世代
の空間にもれでてこないのは道理で、
もし核子が高エネルギーをあたえられて、縁日屋台の
ひも風船のように引き延ばされた場合は、
その力学力線の断面積はどこも一定ですので、
よっていくらはなれても、力の強さはかわらない、
ということになります。
これは、思考としては、電磁力と弱い力が分離する前
の電核力と重力しかなかった時代、
もし宇宙が十分な大きさを持っていれば、その力は逆
2乗の法則に従って伝播していたとも考えられるのかも
しれません。
筆者は高等数学が全く分からないので、数式的にこれ
を理解することができません。
そのころの宇宙が、プランク単位程度の大きさしかな
ければその概念もまた危ういものではありますが。
・重力について
これもまた日経サイエンスのコラムだったと想います。
重力は本当は力ではないのではないか、という
疑念説があります。
別の物理的な機構が裏で働いている作用をあたかもそ
れが力であるように錯覚是認している、
と考えた方が、
論理の上では気が楽になる、
という主張です。
散文的な概念としては筆者はこちらに組したい気がし
ます。
重力をほかの3つの力とおなじものだと仮定して理論
をすすめると、概念的に無理をしなければそれがなりた
たない、といわれるからでもあります。
よく紹介されていた理論として、この世界とは別の存
在の宇宙があって、その宇宙が超次元的に「ちょっかい」
を出しているがゆえに、重力の事象が発生している、と
いうものがあります。
筆者はその話を読んだとき、因果律的にまったく没干
渉であるからこそ、宇宙が別々に存在している理由にな
っているんではないのかと素朴におもったものです。
つまり、この宇宙の事象を説明するのに、常時並行し
て同じような宇宙が存在することが必要なのだという概
念は、数式的要請なのかもしれませんが、あまり考えに
くいものです。
これならばワームホールや孫宇宙の生成という概念の
方がまだわかりやすい構想ではあります。
重力の異常な特徴として、
・+ーという意味での負の符号がない
・ほかの3つの力に比べてそのちからが極端に弱すぎる
その力の比とは、乱暴に言ってしまえば、素粒子と天
体の半径比と言い換えてもいいでしょう。べらぼうな累
乗の値になります。
重力はあるいは時空の性質の一側面なのではないかと
いう気がします。
空間構造の基本理解として、
騾馬電子、あるいはヒッグス粒子という表現がされて
いますが、それが概念的に正しいのかはよくわかりませ
ん。
それらの粒子がべったりと充填しているのが時空だと
説明されていますが、
もし粒子が広義のスピンをもった存在だとすれば、
粒子がべったりと充填された構造というのは、
スピンが部分的にほどけて、金網のようにあみあげら
れた状態が一見静的にみえる宇宙の真空の状態だとみる
ことができます。
この宇宙:真空での粒子の運動というものは、
まずその「泡」の渦巻きのむきが、小さな台風のよう
に逆むきになり、
またその移動とはその泡が、
金網を進行方向に部分的にほどき、
また後方を本来の金網の順法通りの網目にもどし結び
ながら、
金網の網目を、じゃーっと流れていく姿に近いのかも
しれません。
このような時空と粒子がどのように、一見重力のよう
にみえる現象を演出するのか、まったくもってわかりま
せんが、
一つには相対論の挙措が一つのヒントにはなるのかも
しれません。
すなわち
・巨視的には、質量が多く集積すると時空がゆがむ
・ゆがんだ時空は重力という力を及ぼすように見える
このふたつが同じものかどうかは筆者にはよくわかり
ません。
-----
・おまけ(いたずら)
天体の立体図を表現する時に使った概念を披露します。
XYZ軸が、ディスプレイ画面にたがいに60度の角
度で交わっている場合は、3次元の座標を2次元に以下
のように変換すれば俯瞰図を投影することができます。
DispX = Z*cos(0) + Y*cos(+30) + X*cos(-30)
DispY = Z*sin(0) + Y*sin(+30) + X*sin(-30)
Z軸が先頭に立っているのは一般化のためです。
カッコ内の角度も、配列符号的に管理することができ、
0 = 90 - 0*60
+30 = 90 - 1*60
-30 = 90 - 2*60
Z=D(0)、X=D(1)、Y=D(2) とおくと
3-1
DispX or Y = sigma D(k)*cos or sin(90 - k*60)
k=0
と積算記号を使えば一般化できます。
ラジアンで表現すると、
paiは円周率
90 = pai/4, 60 = 2pai/3 ですから
3-1 pai 2pai
DispX or Y = sigma D(k)*cos or sin(--- - ----)
k=0 4 3-1
です。
これをまた、多次元拡張をすると、
n-1 pai 2pai
DispX= sigma D(k) * cos( --- - ----)
k=0 4 n-1
n-1 pai 2pai
DispY= sigma D(k) * sin( --- - ----)
k=0 4 n-1
となり、多次元空間の点をディスプレイに投影できる
ことになります。
たとえばn=4とすると4次元空間の点を投影できます。
この場合は、右半分の象限がディスプレイ上は45度
で交わる4本の座標線で表現されます。
※注意
古来、風景画家は遠景の奥行きを出すことに苦労をし
てきました。3次元を2次元に投影することがもともと
幾何学的に無理があるからです。
人工建築のように単位当たりの区画の長さが一定なも
のであれば、単位長さを距離の反比例にすれば表現は可
能ですが、
自然風景になるともうおてあげです。
かすみの濃度が距離の関数であるということを、無理
に退ければ、空気遠近法は幾何ではありません。
それと同様に4次元以上の幾何体を2次元ディスプレ
イに投影するのがなにか意味があるかどうかはまったく
わかりません。
4次元形式のヤコビの楕円体を2次元ディスプレイに
投影しても、あたまがウニになるだけのような気もしま
すが。
=========================
ファイルの終わり
=========================
 ------------
L = / Xd^2 + Yd^2
すなわち
L^2 = Xd^2 + Yd^2
でもあります。
------
・3次元では、やや複雑になります。
補助線としてのLtmpという長さを導入すれば、これも
一般式を導くことができます。
------------
L = / Xd^2 + Yd^2
すなわち
L^2 = Xd^2 + Yd^2
でもあります。
------
・3次元では、やや複雑になります。
補助線としてのLtmpという長さを導入すれば、これも
一般式を導くことができます。
 Ltmp^2 = Xd^2 + Yd^2
L^2 = Zd^2 + Ltmp^2
= Xd^2 + Yd^2 + Zd^2
-----
・ここから楽観的な拡張をn次元に対して行います。
2次元から3次元に対してZ軸の項が素朴に追加され
たことを、多次元においても一般的に成り立つと強引に
仮定すると、以下の一般式を導くことができます。
L^2 = Xd^2 + Yd^2 + Zd^2 + ... + Ad^2
:A is Any Added Demention
Aは任意の多次元目の座標軸です。
これを数式的に処理しやすいように、配列的に表記す
ると、
n次元空間における、2点間の距離の(二乗)は以下
のように表現できます。
L^2 = D(0)d^2 + D(1)d^2 + D(2)^2 + ... + D(n-1)d^2
n-1
=sigma D(k)d^2
k=0
Dは次元:ディメンションの略です。
-----
・空間における力の減衰に対しての考察
始点の原点(力源)からの距離をDistance1、
終点の力源からの距離を同じく Distance2とします。
結果選出されるそれぞれの力をDyn1Dyn2とします。
議論をわかりやすくするために、力源と始点と終点は
同一直線状にあるとします。
・2次元の場合
Ltmp^2 = Xd^2 + Yd^2
L^2 = Zd^2 + Ltmp^2
= Xd^2 + Yd^2 + Zd^2
-----
・ここから楽観的な拡張をn次元に対して行います。
2次元から3次元に対してZ軸の項が素朴に追加され
たことを、多次元においても一般的に成り立つと強引に
仮定すると、以下の一般式を導くことができます。
L^2 = Xd^2 + Yd^2 + Zd^2 + ... + Ad^2
:A is Any Added Demention
Aは任意の多次元目の座標軸です。
これを数式的に処理しやすいように、配列的に表記す
ると、
n次元空間における、2点間の距離の(二乗)は以下
のように表現できます。
L^2 = D(0)d^2 + D(1)d^2 + D(2)^2 + ... + D(n-1)d^2
n-1
=sigma D(k)d^2
k=0
Dは次元:ディメンションの略です。
-----
・空間における力の減衰に対しての考察
始点の原点(力源)からの距離をDistance1、
終点の力源からの距離を同じく Distance2とします。
結果選出されるそれぞれの力をDyn1Dyn2とします。
議論をわかりやすくするために、力源と始点と終点は
同一直線状にあるとします。
・2次元の場合
 力線が作用する(微小)被作用直行線をL1L2とします。
2次元幾何的に、始点終点の距離の比と、作用を受け
る直行線の比率は同一です。
力の強弱は仮想的な力線がどれだけ被作用線に交差す
るかという密度の概念で決まりますから、2次元では力
の強弱は距離の比に単純に反比例する、という式によっ
て表現することができます。
Distance1:Distance2 = L1:L2 = 1:2
L1 Distance1 1
Dyn2 = Dyn1*---- = Dyn1*--------- = Dyn1*---
L2 Distance2 2
: Dyn1*Distance1 = Dyn2*Distance2 = const
受ける力は、距離に反比例します。
-----
・3次元の場合
力線が作用する(微小)被作用直行線をL1L2とします。
2次元幾何的に、始点終点の距離の比と、作用を受け
る直行線の比率は同一です。
力の強弱は仮想的な力線がどれだけ被作用線に交差す
るかという密度の概念で決まりますから、2次元では力
の強弱は距離の比に単純に反比例する、という式によっ
て表現することができます。
Distance1:Distance2 = L1:L2 = 1:2
L1 Distance1 1
Dyn2 = Dyn1*---- = Dyn1*--------- = Dyn1*---
L2 Distance2 2
: Dyn1*Distance1 = Dyn2*Distance2 = const
受ける力は、距離に反比例します。
-----
・3次元の場合
 力線が作用するのは、線分でなく単位面積になります。
ここまで状況差分を一般化すると、2次元で力線が
作用するのは、単位微線分:1次元、
3次元では、単位微細面積:2次元、
ということになります。
被作用面積をS1S2とすると、
面積比は線分比の二乗になりますから、
力線密度をこの距離比=線分比の二乗で分け合うこと
になり、以下、
Distance1:Distance2 = L1:L2 = 1:2
S1 (Distance1)^2 1
Dyn2 = Dyn1*---- = Dyn1*(---------) = Dyn1*---
S2 (Distance2) 4
: Dyn1*(Distance1)^2 = Dyn2*(Distance2)^2
それぞれの点において、受ける力と距離の二乗の積は
一定、
つまり二次元の世界よりは、離れれば離れるほど受け
る力は弱くなります。
・n次元へ拡張
n次元でも、力線を受ける当該微小単位は
n-1次元の超断面をもつとすると、2,3次元の力の結
論は、次の式に一般化されます。
Dyn1*(Distance1)^(n-1) = Dyn2*(Distance2)^(n-1)
ここで式の概念をわかりやすくするために変形します。
(Distance1)^(n-1) (Distance1)^(n-1) (Distance2)^(-(n-1))
Dyn1*----------------- = Dyn2= Dyn1*(---------) = Dyn1*(---------)
(Distance2)^(n-1) (Distance2) (Distance1)
この式を式*とします。
Distance1、Dyn1の点を、1単位とし、
Distance2、Dyn2の点を、任意の一般点とすると、
その点の距離と受ける力は
DistanceRate、DynRateとなります。
Dyn2 Distance2
DynRate = ----- 式*1 , DistanceRate = --------- 式*2
Dyn1 Distance1
式*2を式*に代入し、
Dyn2 = Dyn1*DistanceRate^(-(n-1))
またこの式の両辺をDyn1で割り、
Dyn2 1
------ = DistanceRate^(-(n-1)) = ------------------
Dyn1 DistanceRate^(n-1)
つまりこれは、
= DynRate
改めて清書すると
1
DynRate = ------------------
DistanceRate^(n-1)
空間次元が上がるほど、遠方で受ける力は
急速に弱くなるようです。
-----
・n次元の任意点
P(D(0)d, D(1)d, D(2)d, ... D(n-1)d)
厳密には始点を原点=力源に置いていますので、差分
を表すdの文字は意味がありません。
差分の意味dを任意点pの意味に書き換えます。
P(D(0)p, D(1)p, D(2)p, ... D(n-1)p)
における、力源=原点を始点とする
長さ1の任意ベクトルが差す任意の点に置ける
力を1とした場合の受ける力を表す式は、
始点が原点であれば、LとDistanceRateは同義ですから、
L = Distantrate
L^2 = D(0)p^2 + D(1)p^2 + D(2)p^2 + ... + D(n-1)p^2
L = ( D(0)p^2 + D(1)p^2 + D(2)p^2 + ... + D(n-1)p^2 )^(1/2)
1 1
DynRate = -------- = --------------------------------------------------------
L^(n-1) (n-1)
(---)
( D(0)p^2 + D(1)p^2 + D(2)p^2 + ... + D(n-1)p^2 )^( 2 )
となります。形式的には。
※これは、太陽系のような中心にほぼ絶対的に重い重
力力点が存在するような系での概念です。
キャベンディシュの実験によってもたらさられた見解
は、地球と分銅の関係において、驚くべきことに分銅に
も引力を発生する力が存在していることです:万有引力。
意味空間のアナロジーの手本となった、星団星雲内の
個々の恒星の相互作用は、それぞれの恒星ごとに重力の
相互作用の積算が存在することであり、
ある星Aがある星Bに対して及ぼす重力の強さを算出す
るばあい、
それぞれの星が距離Lだけ離れている場合は、
その演算においては、Xd、Yd、Zdという距離差分によ
って導き出された力比:DyneRateにその星Aの質量GAを
掛けた値になります。
具体的には、現実宇宙の近似として、
星1000個の恒星星団の場合、ある任意の星A(k)
に対して、
残り1000ー1=999個の星がそれぞれこれらの
差分演算からくる距離と個々の星の重力の積を演算1単
位とし、
それの999個分の重力影響の積算をもって、
それを単位時間ごとの加速度に変換し、
はじめてその任意の星A(k)の微小ステップ移動が算出
されるのです。
また、その任意の星A(k)も、計算ループの別のフェー
ズでは、
また別の星A(kdash)に影響を及ぼす重力源として、作
用に参加するのです。
・・・人間の考えることはそんなに特別なことではな
いはずですから、人工知能の単語空間における意味演算
もまたほとんどおなじプロセスをたどっているはずと推
測はしますが、
ただこの総当たり式のシミュレーションはおそろしく
べらぼうな演算量を必要とします。
3次元空間の星1000個の星団での演算は、
それぞれの星一つについてののこり999個の恒星の
重力影響の積算演算を、
全1000個の星ごとに行ってはじめて1ステップの
計算が終了するのです。
つまり、およそ
1000^2=10^(3+2)=10^5=10万演算
それが、計算精度を上げるためには、1ステップをで
きるだけ微細な時間単位を取らなければならないので、
なかなか演算が進捗しません。
星雲のシミュレーションも、人工知能も、
想像を絶する計算力を必要としますので、
このようなことが可能となったのは、やはりごく最近
になってからだ、ということはできるでしょう。
参考経験:多体問題999:思い切り手前味噌。
たしかソースコードはつけていたはずですので興味が
あるならどうぞ。
*
少し随想。
・力の作用が弱い高次元空間
素朴なこの数式を扱っておもったのは、高次元の空間
とは、ちょっと離れただけで重力などがほとんど作用し
なくなっている空間だということがわかります。
原子は電磁気力による電子の軌道、天体は重力による
惑星系や衛星の軌道、
高次元とはつまりこのようなものが存在しにくい空間
だとも考えられます。
ある程度高い次元の空間とは、素粒子がただスープの
ようにただようだけの、ほとんど事象がなにも起こらな
い空間だということも言えます。
そのような記述をどこかで読んだ記憶があります。
日経サイエンスだとは思いますが、
弱い人間原理に照らせば、この宇宙が3次元空間なの
は、ほかの高い次元では、生命を生むだけの物質の相互
作用がほとんど起きないからだ、と帰納することができ
るのかもしれません。
また2次元以下の宇宙では、影響力が逆に固くつぶれ
てしまって、窒息がごとくにこれも何も起きにくい世界
なのかもしれません。
どういう数学的背景なのかは多分筆者には理解できな
いと思いますが、この宇宙はもともと11次元であり、
のこりの次元は素粒子レベルの泡となってまるまってい
て、日常的な感覚では知覚できないからだという説もあ
ります。
そうだとするのならば、もともと多次元宇宙として始
まったこの宇宙が、何の因果か、それこそ事象現象の十
分な成立を優先させたがために、変形を進化というのは
微妙ですが、すくなくとも変化したともいえるのでしょ
うか?
・グルーオンについて
強い力というものは、距離がどこまで伸びてもその力
は一定だ、と核物理の入門書にはかいてあります。
素朴な感覚として、3次元空間にそんな力は存在しな
いはずです。
これも、たぶんどこかで読んだ記事だと思いますが、
強い力というものは素朴な意味でのこの宇宙空間の力で
はなく、相転移するまえの古い宇宙空間独特の力であり、
いわゆる核子、重粒子:ハドロンとは、
その相転移するまえの古い宇宙空間が断片化されて、
あたかも濡れた化繊のシャツが肌に張り付くときに、微
小な空気が閉じ込められて、線状の微細な個々のしわに
なるように、
現在の広大な宇宙空間に、閉じ込められた状態だ、
とするものです。
ハドロンの内側、
別の空間の別種の力であれば、それがこの新しい世代
の空間にもれでてこないのは道理で、
もし核子が高エネルギーをあたえられて、縁日屋台の
ひも風船のように引き延ばされた場合は、
その力学力線の断面積はどこも一定ですので、
よっていくらはなれても、力の強さはかわらない、
ということになります。
これは、思考としては、電磁力と弱い力が分離する前
の電核力と重力しかなかった時代、
もし宇宙が十分な大きさを持っていれば、その力は逆
2乗の法則に従って伝播していたとも考えられるのかも
しれません。
筆者は高等数学が全く分からないので、数式的にこれ
を理解することができません。
そのころの宇宙が、プランク単位程度の大きさしかな
ければその概念もまた危ういものではありますが。
・重力について
これもまた日経サイエンスのコラムだったと想います。
重力は本当は力ではないのではないか、という
疑念説があります。
別の物理的な機構が裏で働いている作用をあたかもそ
れが力であるように錯覚是認している、
と考えた方が、
論理の上では気が楽になる、
という主張です。
散文的な概念としては筆者はこちらに組したい気がし
ます。
重力をほかの3つの力とおなじものだと仮定して理論
をすすめると、概念的に無理をしなければそれがなりた
たない、といわれるからでもあります。
よく紹介されていた理論として、この世界とは別の存
在の宇宙があって、その宇宙が超次元的に「ちょっかい」
を出しているがゆえに、重力の事象が発生している、と
いうものがあります。
筆者はその話を読んだとき、因果律的にまったく没干
渉であるからこそ、宇宙が別々に存在している理由にな
っているんではないのかと素朴におもったものです。
つまり、この宇宙の事象を説明するのに、常時並行し
て同じような宇宙が存在することが必要なのだという概
念は、数式的要請なのかもしれませんが、あまり考えに
くいものです。
これならばワームホールや孫宇宙の生成という概念の
方がまだわかりやすい構想ではあります。
重力の異常な特徴として、
・+ーという意味での負の符号がない
・ほかの3つの力に比べてそのちからが極端に弱すぎる
その力の比とは、乱暴に言ってしまえば、素粒子と天
体の半径比と言い換えてもいいでしょう。べらぼうな累
乗の値になります。
重力はあるいは時空の性質の一側面なのではないかと
いう気がします。
空間構造の基本理解として、
騾馬電子、あるいはヒッグス粒子という表現がされて
いますが、それが概念的に正しいのかはよくわかりませ
ん。
それらの粒子がべったりと充填しているのが時空だと
説明されていますが、
もし粒子が広義のスピンをもった存在だとすれば、
粒子がべったりと充填された構造というのは、
スピンが部分的にほどけて、金網のようにあみあげら
れた状態が一見静的にみえる宇宙の真空の状態だとみる
ことができます。
この宇宙:真空での粒子の運動というものは、
まずその「泡」の渦巻きのむきが、小さな台風のよう
に逆むきになり、
またその移動とはその泡が、
金網を進行方向に部分的にほどき、
また後方を本来の金網の順法通りの網目にもどし結び
ながら、
金網の網目を、じゃーっと流れていく姿に近いのかも
しれません。
このような時空と粒子がどのように、一見重力のよう
にみえる現象を演出するのか、まったくもってわかりま
せんが、
一つには相対論の挙措が一つのヒントにはなるのかも
しれません。
すなわち
・巨視的には、質量が多く集積すると時空がゆがむ
・ゆがんだ時空は重力という力を及ぼすように見える
このふたつが同じものかどうかは筆者にはよくわかり
ません。
-----
・おまけ(いたずら)
天体の立体図を表現する時に使った概念を披露します。
XYZ軸が、ディスプレイ画面にたがいに60度の角
度で交わっている場合は、3次元の座標を2次元に以下
のように変換すれば俯瞰図を投影することができます。
DispX = Z*cos(0) + Y*cos(+30) + X*cos(-30)
DispY = Z*sin(0) + Y*sin(+30) + X*sin(-30)
Z軸が先頭に立っているのは一般化のためです。
カッコ内の角度も、配列符号的に管理することができ、
0 = 90 - 0*60
+30 = 90 - 1*60
-30 = 90 - 2*60
Z=D(0)、X=D(1)、Y=D(2) とおくと
3-1
DispX or Y = sigma D(k)*cos or sin(90 - k*60)
k=0
と積算記号を使えば一般化できます。
ラジアンで表現すると、
paiは円周率
90 = pai/4, 60 = 2pai/3 ですから
3-1 pai 2pai
DispX or Y = sigma D(k)*cos or sin(--- - ----)
k=0 4 3-1
です。
これをまた、多次元拡張をすると、
n-1 pai 2pai
DispX= sigma D(k) * cos( --- - ----)
k=0 4 n-1
n-1 pai 2pai
DispY= sigma D(k) * sin( --- - ----)
k=0 4 n-1
となり、多次元空間の点をディスプレイに投影できる
ことになります。
たとえばn=4とすると4次元空間の点を投影できます。
この場合は、右半分の象限がディスプレイ上は45度
で交わる4本の座標線で表現されます。
※注意
古来、風景画家は遠景の奥行きを出すことに苦労をし
てきました。3次元を2次元に投影することがもともと
幾何学的に無理があるからです。
人工建築のように単位当たりの区画の長さが一定なも
のであれば、単位長さを距離の反比例にすれば表現は可
能ですが、
自然風景になるともうおてあげです。
かすみの濃度が距離の関数であるということを、無理
に退ければ、空気遠近法は幾何ではありません。
それと同様に4次元以上の幾何体を2次元ディスプレ
イに投影するのがなにか意味があるかどうかはまったく
わかりません。
4次元形式のヤコビの楕円体を2次元ディスプレイに
投影しても、あたまがウニになるだけのような気もしま
すが。
=========================
ファイルの終わり
=========================
力線が作用するのは、線分でなく単位面積になります。
ここまで状況差分を一般化すると、2次元で力線が
作用するのは、単位微線分:1次元、
3次元では、単位微細面積:2次元、
ということになります。
被作用面積をS1S2とすると、
面積比は線分比の二乗になりますから、
力線密度をこの距離比=線分比の二乗で分け合うこと
になり、以下、
Distance1:Distance2 = L1:L2 = 1:2
S1 (Distance1)^2 1
Dyn2 = Dyn1*---- = Dyn1*(---------) = Dyn1*---
S2 (Distance2) 4
: Dyn1*(Distance1)^2 = Dyn2*(Distance2)^2
それぞれの点において、受ける力と距離の二乗の積は
一定、
つまり二次元の世界よりは、離れれば離れるほど受け
る力は弱くなります。
・n次元へ拡張
n次元でも、力線を受ける当該微小単位は
n-1次元の超断面をもつとすると、2,3次元の力の結
論は、次の式に一般化されます。
Dyn1*(Distance1)^(n-1) = Dyn2*(Distance2)^(n-1)
ここで式の概念をわかりやすくするために変形します。
(Distance1)^(n-1) (Distance1)^(n-1) (Distance2)^(-(n-1))
Dyn1*----------------- = Dyn2= Dyn1*(---------) = Dyn1*(---------)
(Distance2)^(n-1) (Distance2) (Distance1)
この式を式*とします。
Distance1、Dyn1の点を、1単位とし、
Distance2、Dyn2の点を、任意の一般点とすると、
その点の距離と受ける力は
DistanceRate、DynRateとなります。
Dyn2 Distance2
DynRate = ----- 式*1 , DistanceRate = --------- 式*2
Dyn1 Distance1
式*2を式*に代入し、
Dyn2 = Dyn1*DistanceRate^(-(n-1))
またこの式の両辺をDyn1で割り、
Dyn2 1
------ = DistanceRate^(-(n-1)) = ------------------
Dyn1 DistanceRate^(n-1)
つまりこれは、
= DynRate
改めて清書すると
1
DynRate = ------------------
DistanceRate^(n-1)
空間次元が上がるほど、遠方で受ける力は
急速に弱くなるようです。
-----
・n次元の任意点
P(D(0)d, D(1)d, D(2)d, ... D(n-1)d)
厳密には始点を原点=力源に置いていますので、差分
を表すdの文字は意味がありません。
差分の意味dを任意点pの意味に書き換えます。
P(D(0)p, D(1)p, D(2)p, ... D(n-1)p)
における、力源=原点を始点とする
長さ1の任意ベクトルが差す任意の点に置ける
力を1とした場合の受ける力を表す式は、
始点が原点であれば、LとDistanceRateは同義ですから、
L = Distantrate
L^2 = D(0)p^2 + D(1)p^2 + D(2)p^2 + ... + D(n-1)p^2
L = ( D(0)p^2 + D(1)p^2 + D(2)p^2 + ... + D(n-1)p^2 )^(1/2)
1 1
DynRate = -------- = --------------------------------------------------------
L^(n-1) (n-1)
(---)
( D(0)p^2 + D(1)p^2 + D(2)p^2 + ... + D(n-1)p^2 )^( 2 )
となります。形式的には。
※これは、太陽系のような中心にほぼ絶対的に重い重
力力点が存在するような系での概念です。
キャベンディシュの実験によってもたらさられた見解
は、地球と分銅の関係において、驚くべきことに分銅に
も引力を発生する力が存在していることです:万有引力。
意味空間のアナロジーの手本となった、星団星雲内の
個々の恒星の相互作用は、それぞれの恒星ごとに重力の
相互作用の積算が存在することであり、
ある星Aがある星Bに対して及ぼす重力の強さを算出す
るばあい、
それぞれの星が距離Lだけ離れている場合は、
その演算においては、Xd、Yd、Zdという距離差分によ
って導き出された力比:DyneRateにその星Aの質量GAを
掛けた値になります。
具体的には、現実宇宙の近似として、
星1000個の恒星星団の場合、ある任意の星A(k)
に対して、
残り1000ー1=999個の星がそれぞれこれらの
差分演算からくる距離と個々の星の重力の積を演算1単
位とし、
それの999個分の重力影響の積算をもって、
それを単位時間ごとの加速度に変換し、
はじめてその任意の星A(k)の微小ステップ移動が算出
されるのです。
また、その任意の星A(k)も、計算ループの別のフェー
ズでは、
また別の星A(kdash)に影響を及ぼす重力源として、作
用に参加するのです。
・・・人間の考えることはそんなに特別なことではな
いはずですから、人工知能の単語空間における意味演算
もまたほとんどおなじプロセスをたどっているはずと推
測はしますが、
ただこの総当たり式のシミュレーションはおそろしく
べらぼうな演算量を必要とします。
3次元空間の星1000個の星団での演算は、
それぞれの星一つについてののこり999個の恒星の
重力影響の積算演算を、
全1000個の星ごとに行ってはじめて1ステップの
計算が終了するのです。
つまり、およそ
1000^2=10^(3+2)=10^5=10万演算
それが、計算精度を上げるためには、1ステップをで
きるだけ微細な時間単位を取らなければならないので、
なかなか演算が進捗しません。
星雲のシミュレーションも、人工知能も、
想像を絶する計算力を必要としますので、
このようなことが可能となったのは、やはりごく最近
になってからだ、ということはできるでしょう。
参考経験:多体問題999:思い切り手前味噌。
たしかソースコードはつけていたはずですので興味が
あるならどうぞ。
*
少し随想。
・力の作用が弱い高次元空間
素朴なこの数式を扱っておもったのは、高次元の空間
とは、ちょっと離れただけで重力などがほとんど作用し
なくなっている空間だということがわかります。
原子は電磁気力による電子の軌道、天体は重力による
惑星系や衛星の軌道、
高次元とはつまりこのようなものが存在しにくい空間
だとも考えられます。
ある程度高い次元の空間とは、素粒子がただスープの
ようにただようだけの、ほとんど事象がなにも起こらな
い空間だということも言えます。
そのような記述をどこかで読んだ記憶があります。
日経サイエンスだとは思いますが、
弱い人間原理に照らせば、この宇宙が3次元空間なの
は、ほかの高い次元では、生命を生むだけの物質の相互
作用がほとんど起きないからだ、と帰納することができ
るのかもしれません。
また2次元以下の宇宙では、影響力が逆に固くつぶれ
てしまって、窒息がごとくにこれも何も起きにくい世界
なのかもしれません。
どういう数学的背景なのかは多分筆者には理解できな
いと思いますが、この宇宙はもともと11次元であり、
のこりの次元は素粒子レベルの泡となってまるまってい
て、日常的な感覚では知覚できないからだという説もあ
ります。
そうだとするのならば、もともと多次元宇宙として始
まったこの宇宙が、何の因果か、それこそ事象現象の十
分な成立を優先させたがために、変形を進化というのは
微妙ですが、すくなくとも変化したともいえるのでしょ
うか?
・グルーオンについて
強い力というものは、距離がどこまで伸びてもその力
は一定だ、と核物理の入門書にはかいてあります。
素朴な感覚として、3次元空間にそんな力は存在しな
いはずです。
これも、たぶんどこかで読んだ記事だと思いますが、
強い力というものは素朴な意味でのこの宇宙空間の力で
はなく、相転移するまえの古い宇宙空間独特の力であり、
いわゆる核子、重粒子:ハドロンとは、
その相転移するまえの古い宇宙空間が断片化されて、
あたかも濡れた化繊のシャツが肌に張り付くときに、微
小な空気が閉じ込められて、線状の微細な個々のしわに
なるように、
現在の広大な宇宙空間に、閉じ込められた状態だ、
とするものです。
ハドロンの内側、
別の空間の別種の力であれば、それがこの新しい世代
の空間にもれでてこないのは道理で、
もし核子が高エネルギーをあたえられて、縁日屋台の
ひも風船のように引き延ばされた場合は、
その力学力線の断面積はどこも一定ですので、
よっていくらはなれても、力の強さはかわらない、
ということになります。
これは、思考としては、電磁力と弱い力が分離する前
の電核力と重力しかなかった時代、
もし宇宙が十分な大きさを持っていれば、その力は逆
2乗の法則に従って伝播していたとも考えられるのかも
しれません。
筆者は高等数学が全く分からないので、数式的にこれ
を理解することができません。
そのころの宇宙が、プランク単位程度の大きさしかな
ければその概念もまた危ういものではありますが。
・重力について
これもまた日経サイエンスのコラムだったと想います。
重力は本当は力ではないのではないか、という
疑念説があります。
別の物理的な機構が裏で働いている作用をあたかもそ
れが力であるように錯覚是認している、
と考えた方が、
論理の上では気が楽になる、
という主張です。
散文的な概念としては筆者はこちらに組したい気がし
ます。
重力をほかの3つの力とおなじものだと仮定して理論
をすすめると、概念的に無理をしなければそれがなりた
たない、といわれるからでもあります。
よく紹介されていた理論として、この世界とは別の存
在の宇宙があって、その宇宙が超次元的に「ちょっかい」
を出しているがゆえに、重力の事象が発生している、と
いうものがあります。
筆者はその話を読んだとき、因果律的にまったく没干
渉であるからこそ、宇宙が別々に存在している理由にな
っているんではないのかと素朴におもったものです。
つまり、この宇宙の事象を説明するのに、常時並行し
て同じような宇宙が存在することが必要なのだという概
念は、数式的要請なのかもしれませんが、あまり考えに
くいものです。
これならばワームホールや孫宇宙の生成という概念の
方がまだわかりやすい構想ではあります。
重力の異常な特徴として、
・+ーという意味での負の符号がない
・ほかの3つの力に比べてそのちからが極端に弱すぎる
その力の比とは、乱暴に言ってしまえば、素粒子と天
体の半径比と言い換えてもいいでしょう。べらぼうな累
乗の値になります。
重力はあるいは時空の性質の一側面なのではないかと
いう気がします。
空間構造の基本理解として、
騾馬電子、あるいはヒッグス粒子という表現がされて
いますが、それが概念的に正しいのかはよくわかりませ
ん。
それらの粒子がべったりと充填しているのが時空だと
説明されていますが、
もし粒子が広義のスピンをもった存在だとすれば、
粒子がべったりと充填された構造というのは、
スピンが部分的にほどけて、金網のようにあみあげら
れた状態が一見静的にみえる宇宙の真空の状態だとみる
ことができます。
この宇宙:真空での粒子の運動というものは、
まずその「泡」の渦巻きのむきが、小さな台風のよう
に逆むきになり、
またその移動とはその泡が、
金網を進行方向に部分的にほどき、
また後方を本来の金網の順法通りの網目にもどし結び
ながら、
金網の網目を、じゃーっと流れていく姿に近いのかも
しれません。
このような時空と粒子がどのように、一見重力のよう
にみえる現象を演出するのか、まったくもってわかりま
せんが、
一つには相対論の挙措が一つのヒントにはなるのかも
しれません。
すなわち
・巨視的には、質量が多く集積すると時空がゆがむ
・ゆがんだ時空は重力という力を及ぼすように見える
このふたつが同じものかどうかは筆者にはよくわかり
ません。
-----
・おまけ(いたずら)
天体の立体図を表現する時に使った概念を披露します。
XYZ軸が、ディスプレイ画面にたがいに60度の角
度で交わっている場合は、3次元の座標を2次元に以下
のように変換すれば俯瞰図を投影することができます。
DispX = Z*cos(0) + Y*cos(+30) + X*cos(-30)
DispY = Z*sin(0) + Y*sin(+30) + X*sin(-30)
Z軸が先頭に立っているのは一般化のためです。
カッコ内の角度も、配列符号的に管理することができ、
0 = 90 - 0*60
+30 = 90 - 1*60
-30 = 90 - 2*60
Z=D(0)、X=D(1)、Y=D(2) とおくと
3-1
DispX or Y = sigma D(k)*cos or sin(90 - k*60)
k=0
と積算記号を使えば一般化できます。
ラジアンで表現すると、
paiは円周率
90 = pai/4, 60 = 2pai/3 ですから
3-1 pai 2pai
DispX or Y = sigma D(k)*cos or sin(--- - ----)
k=0 4 3-1
です。
これをまた、多次元拡張をすると、
n-1 pai 2pai
DispX= sigma D(k) * cos( --- - ----)
k=0 4 n-1
n-1 pai 2pai
DispY= sigma D(k) * sin( --- - ----)
k=0 4 n-1
となり、多次元空間の点をディスプレイに投影できる
ことになります。
たとえばn=4とすると4次元空間の点を投影できます。
この場合は、右半分の象限がディスプレイ上は45度
で交わる4本の座標線で表現されます。
※注意
古来、風景画家は遠景の奥行きを出すことに苦労をし
てきました。3次元を2次元に投影することがもともと
幾何学的に無理があるからです。
人工建築のように単位当たりの区画の長さが一定なも
のであれば、単位長さを距離の反比例にすれば表現は可
能ですが、
自然風景になるともうおてあげです。
かすみの濃度が距離の関数であるということを、無理
に退ければ、空気遠近法は幾何ではありません。
それと同様に4次元以上の幾何体を2次元ディスプレ
イに投影するのがなにか意味があるかどうかはまったく
わかりません。
4次元形式のヤコビの楕円体を2次元ディスプレイに
投影しても、あたまがウニになるだけのような気もしま
すが。
=========================
ファイルの終わり
=========================