======================================== ピタゴラスの定理と球と円錐（レポート） CopyRight miyama.2012 April - May Ver0.01 kaz_kimijima@yahoo.co.jp www.geocities.jp/kaz_kimijia ======================================== はじめに これは研究というよりはレポートです 数学に関してはいままで独自的なものをま とめたものをいわば小論文のまねごととして 上梓してきましたが、 今回は自分が個人的に疑問に想っていた問 題を既存の資料などをなぞって考えを確かめ たもの結したものであり、今回は筆者の独自 性は乏しいレポートになります 今回は独自性のある記事は小発見として一 項目しかありません ただ、今日の電子時代において考えをまと めたものを死蔵するのも手間としてもったい ないかなとおもい、ここに後学氏のご参考ま でに上梓したいとおもいます。 ＊ 履修問題上、使用することの多い定理のひ とつとしてピタゴラスの定理があります しかし筆者がそうだったように、多くの人 々がこの定理の研修的な証明を知ることなし に使っていることが多いのではないかと想い ます 受験に追われていた頃は、ともかく時間が ありませんでしたので、筆者もその公理に対 して素朴に童心のような疑問を抱くことはで きませんでした またのちになって、この公理の証明を文献 として探してみましたが、探し方も悪かった のでしょうが二、三の図書館の蔵書の範囲で は見つけることができませんでした ここではこの定理を初等幾何の範囲で証明 した記事をはじめにその他の数学上の定理に 言及します：筆者の独自性はこの定理の証明 だけです 現代は、オンラインのデータベースが充実 している時代ですので、このような試行は後 学氏はしないでもすむのかもしれませんが、 それはそれで不幸なことなのかもしれません いっけんなんでもある時代は、自分で格闘 するモチベーションがなかなか生まれません。 「充満もまた空虚である」デカルトならある いはこういったかもしれませんね。 なお、この稿を書いていてふとくだらない ことに気づきましたが、筆者の下の名前は別 に数学マニアを名乗っているものではありま せん、そう受け取る人がいるのかもしれない な、と危惧した次第です その意味では、名前負けもはなはだしいで す、ああ恥ずかしい。 また、いうまでもありませんがピタゴラス とはシアノメタクリレート系瞬間接着剤のＣ Ｆに出ていた人ではありません （ぴたーっゴラス） 使用許認可条件 フリードキュメントです 閲覧配布は自由です 動作機器条件 HTML3.0以上のブラウザ動作環境であれば WINMACを問いません 使用方法 アーカイブを解凍してできるフォルダには 図表の画像が入っています コピーする場合はいっしょに移動してくだ さい 免責 このドキュメントの内容を酔席で開陳した り、試験レポートに転載して生じたあらゆる 不具合不都合に対して著者は責任を負いませ ん あらかじめご了承ください ---------------------------------------- 本編内容 １ピタゴラスの定理 ２球の体積について 定積分で求める 球の体積を初等幾何で求める（別解） 区分求積法としてのカバリエリの原理 三角形の面積 錐体の体積 定積分としての球の円筒と円錐への分割 円筒と円錐の関係をピタゴラスの定理の 周辺から考察する 球の積分と円の積分の違い ３球の表面積について 回転体の表面積をもとめるための考察 曲線の長さを求める積分について 曲線関数としての円弧の長さを求める 円弧の微細屋根長さΔrを求める 円弧の回転積分として半球の表面積を得る 付記 微細円筒近似の傍検証 付記 円錐微細部分による近似 円錐の表面積：直接には式未使用 備考：微分における円弧の性質 ：直交する、接線と半径としての法線 円錐の縦断面三角形としての円弧の接線と x軸との交点から円錐斜面の辺半径を求める 微細円錐面積積分としての近似式の作成 ：この方法での表面積の算出 「円の面積を求めるためのぎざぎざ法」 ４ピタゴラス派の秘密主義と時代背景 ：円弧の積分と超越数的性質 ---------------------------------------- １ピタゴラスの定理 r^2 = a^2 + b^2 いわゆるピタゴラスの定理はこの方程式で 示されます ちょっとみると単純な形式にみえますが、 単純な物事こそ用心して考えた方が方法論 としては、賢明かもしれません 理系的思考の訓練をしていない人の社会的 行動を後ろから見ていてときどきおもってい たことなのですが、（多忙でもあり立ち止ま って考える習慣を避けないのは仕方のないこ とかもしれませんが）物事を奥行きを持って 考えるという習慣は、モダンタイムズの時代 の工員でもある近代人には失われているもの なのかもしれないなと筆者は想っていました 露頭だけをみて、鉱脈を想像できないのは おそらく近代人の特徴です 佐渡島に、露頭からどんどん掘り進めて、 ついには山を縦に断ち割ってしまった壮大 な遺構があります ゲーテはベートーベンの同時代人ですので おそらく１８世紀末の人ですが、氏の言葉に 「唯一の技能のみ鍛錬したまえ、これからは その様な時代がくるのだ」という言葉があり ます これは要するに良い意味でも悪い意味でも、 社会の歯車になっても生きていける時代がく るということです このような社会では、青写真や戦略を立て る側もひとつの専門技能になりますから 逆に雇われものの側もまた分化された職業 以外のことを考慮しなくてもすむ時代という ことです その意味では近代とは工員の時代と言うこ とであり、２０世紀の悲劇のひとつは、認識 世界の狭い工員による民主主義の暴走と言う 面がありました ゲーテ氏自身の内面はもちろん狭いもので はありません そして第三世界が今現在総力をあげて工業 化している最中ですが、この時勢が大体飽和 した時点を持っておそらくこの惑星の近代と いう時代は終わりを告げるのでしょう 近代が終われば、否が応でも人々はいわゆ る「総合人」であることを要求される時代に なります これはなにも形而上学の上の話ではなくて、 具体的な求職の意味でも「何でもできなけれ ば生き残れない」ということです 冷静に考えてみると、とんでもないパラダ イムの転換、ということでしょうね これはいわばゲーテの言葉の時代が約三世 紀、実質２５０年ほどを経ておわりつつある、 ということを意味します 我々が直面している沈滞感覚とは、コンド ラチェフの循環という一時的な経済気象など ではなくて、もっと大きな文明の屋台骨の転 換というものです たとえば、古い旧家では、家の生垣に茶の 木を植え、また米にむかない乾いた土地には 麦を植え、うどんなどを打ってできるだけ自 分たちの領家で衣食住が回るように工夫して いました なんでもできること、のニーズとしての基 本は、求職があるかどうかわからない技能の 資格をやみくもに集めることではなくて、 自分たちの生活や仕事に必要なことをいま ある資産でできるだけ工夫することが源泉と しては、本来のような気がします まず、ホームセンターに行きましょう 笑 雇用される態度や、レディメイドの情報に だけすがる態度にのみなれてしまっていると たとえば、独立してラーメン店をはじめるよ うな場合、路地ひとつの集客力のちがいだけ で他方は支店を出すほど繁盛するのに、片方 はたった３ヶ月で撤退、とい痛い分水嶺にな ったりします 教条主義にさえ陥らなければ、嗅覚や直感 を訓練する論理的な思考の形式になじむこと は、けっして損ではありません 業界への攻撃と受け取られてしまうと困る のですが、少なくとも若いうちは漫画よりも 活字を読んだ方が、すくなくともそういう意 味では青春の肥やしになるようです ピタゴラスの定理は円の方程式と同じ形式 を示しています r^2 = x^2 + y^2 円は概念として円周率と同義でありますが、 円周率は超越数というある特殊な種類の数に 属していて、この超越数という数はそのなか に定義上の無限を内包しています 円周率とはすなわち π = 3.1415..... です 次の図は多くの所でよくみるピタゴラスの 定理の図です
図１ ピタゴラスの定理の古典的な図 この定理の不思議を解きたいなとばくぜん と想っていたとき、筆者はまずこの古典的な 教科書にも載っている図を連想しました この図をはじめてみたときは、筆者は中学 生でした しかしこの図からではピタゴラスの定理を 証明として解くことはできませんでした この図には解法のためのヒントになる論理 的補助線が含まれていないからです ２０１２年初頭に自分はこの証明を偶然解 くことができました もしよい書籍とめぐり合っていれば私は幼 少期にすでにこの証明を知っていたことでし ょう 一度わかってしまえばその図による証明は ひどく単純なものでした 具体的な社会経験も訓練もできていなかっ た高校生までの自分ではこの単純な証明を思 いつくことは、たぶんできなかったでしょう 具体的なカリキュラムのどの辺りまでのこ とを示すのかは分かりませんが、たしかにあ る程度の高等教育は具体的な経験がないと意 味がない場合があるものかもしれません その図を次に示します
図２ 拡張したピタゴラスの定理の図 この図を見れば単純な初等幾何の面積の和 の式により定理が導けることがことがわかる とおもいます この図形は大きな外側の正方形に内側の正 方形が四点で内接をしています 内側の正方形の一般の長さをr、 内側の正方形によって占められたあまりの ４つの直角三角形のこの図では長いほうの辺 の長さをa、短い方をbとします 辺の名前で構成した直角三角形rab各ひとつ の面積は明らかに (1/2)*(a*b) であり すべての図形を内包する一番大きな正方形 の面積は当然 (a+b)^2 です ここで、初等的にそれぞれの面積和を式化 すると、 直角三角形は４つ、一辺がrである正方形 がひとつでありますから a*b (a+b)^2 = r^2 + 4{-----} 2 となり展開して a^2 + b^2 + 2ab = r^2 + 2ab 双方の辺にふくまれている項2abが衝突消 滅して、 a^2 + b^2 = r^2 が得られます ピタゴラスの定理そのものの初等証明は これで解決できました なお、この図は球の体積を求める問題に おいてもう一度後にでてきます ２球の体積について 個人的に別の動機で調べていた球の体積 と表面積を求める問題に、おそらくピタゴ ラスの定理が円の定義でもある理由からで しょうか、顔を出しているのに気づいてい ました ここではその試行をまとめて書き連ねた いと想います ２−１定積分で求める 以下は高校教科書の大人の意識による再解 釈になります 積分法を用いて考えますので、座標図を示 します
図３ 球の定積分の図 任意の半径rをもつ円を考えます これは次の方程式を持ちます x^2 + y^2 = r^2 この円の半分、つまりx軸の正値の区間を 0からrにとり、この円の回転体としての体積 積分を、その定積分で考えます この方程式円弧上の任意の点を P(xp,yp) とおき、 この点を外周円に含む微細厚さdxの回転円 盤を考えます 区分求積法の概念により、集積される微細 円盤の微細体積ΔVの一般形を考えると、 ΔV = π*yp^2*dx ですからこれを定積分し 半球の体積の式は |r |r |ΔV = | π * yp^2 dx |0 |0 |r __________ =π| (/r^2 - xp^2)^2 dx |0 重要： ここで平方根と円板面積としての二乗が偶 然相殺し、 |r =π| r^2 - xp^2 dx |0 となります ここで p(xp,yp) -> (x,y) と一般化すると |r =π| r^2 - x^2 dx |0 となり、これは単純に整関数の積分になり ますから | x^3|r =π|r^2 - ---| | 3 |0 r^3 =π(r^3 - --- +0-0) 3 2 =π-r^3 3 これは半球の体積ですから 全球の体積はその２倍で、 4 V = π-r^3 3 となります これで球の体積式も求めることができました ２−２球の体積を初等幾何で求める（別解） ２−２−１三角形の面積 小学校で、私たちは三角形や平行四辺形の 面積を求める方法を学びました もちろん平行四辺形は 底辺＊高さ で面積が表示され、 任意の合同な三角形のむきが逆な合体が平 行四辺形ですから、その面積を二分して三角 形の面積は 底辺＊高さ/2 です
図４ 平行四辺形と三角形の面積 これは式が示す通り、たとえ三角形がひど く傾いていても、その高さと底辺の長ささえ 同じならその面積は等しいことを示します
図５ 形の異なる三角形の面積 この発想がおそらく積分の区分求積法の基 となったカバリエリの原理の本貫でしょう その原理の本質を三角形の面積の求法で言 えば、 底辺を基線として面積を矩形に分割すれば、 これを横にひどくスライドさせてもその総和 積分の値は一定である、という発想です
図６ 三角形の面積における積分の概念の萌芽 ２−２−２錐体の体積 矩形の概念をしばしば不定形な円盤に拡張 すれば、この概念は錐体の体積の求法になり ます
図７ 錐体の体積と底面積の関係 すなわち、錐体の体積はその底面積と高さ の積に比例し、それはたとえば底辺を正方形 である角錐と体積が一致する思考の試行を通 して、 底面積＊高さ/3 と導くことができます オンライン辞典によれば 正六面体を、中心点を通る切り口で六分割 すると一辺のながさをLとした場合
図８ 正六面体の六分割 高さ h = L/2 底面の正方形の面積 s = L^2 また六分割ですので錐体の体積は V = L^3/6 ですから 任意係数をkとし、 V = k * hs L^3 L^3 --- = k--- 6 2 よって k = 1/3 という証明がなりたつようです ２−２−３定積分としての球の円筒と円錐 への分割 オンライン辞典による証明では、この概念 を発展して、 それぞれ、底面円の面積と高さが等しい 半球の体積は 円筒の体積から円錐の体積を引いたもの であることを利用して、半球の体積を導いて いました もちろん積分法の代数を使って示すことも できます 定積分で記述すると、 |r π| r^2-x^2 dx 式A |0 が半球の体積を求める与式ですが、これは |r |r =π| r^2 dx - π|x^2 dx 式B |0 |0 となり、これは底面円の半径をｒとした 場合、 高さｒの円筒の体積から高さｒの円錐の 体積を減算したものになります
図９ 球の体積＝円筒の体積−円錐の体積 特に積分代数の知識がなくとも、この場合 円錐の体積はこの円筒の1/3の体積で すから、残りは2/3, よって半球の体積は πr^2 *r *2/3 = πr^3*2/3 底面積 高さ となります これを２倍して全球化すると体積は 4 -πr^3 3 となります 円筒と円錐に分割するというこの概念は 上記の式Bの概念ですが、これは微細体積ΔV の定積分である式Aからの帰結であり、 ΔV自体が ΔV = 円筒円盤 - 円錐円盤 という性格をもっています これはそのまま = 定数rの二乗 - 変数xの二乗 という形式であり、代数的には球の方程式 の変形に他ならないのですが、 直感的には不思議な気がしますね ２−２−４円筒と円錐の関係をピタゴラス の定理の周辺から考察する この項目では、前項の 円筒円盤と円錐円盤 が出発点となります この円筒と円錐の関係を、その断面を底面 から上方へたとえば動画で移動したとすると、 それは境界を示す円が周囲から中心にむかっ て縮小し最後は微細点となって消滅するよう な映像となって映るでしょう 点となって消滅する…というところでぴん ときました 今年の当初にピタゴラスの定理で思いつい ていた正方形の図を思い出しました ピタゴラスの定理を考えていたときに、前 項の正方形において、複雑な多くの補助線を 引いていた試行のひとつに、 基本三角形の斜辺がいわばロータリーエン ジンの回転子のように回っていく過程で、 回転のある一点でその大きさがゼロになる 中央の正方形があることを気がついていたので す
図１０ ピタゴラスの定理拡張図 図１１−１３ 以下rの値による２次内包正 方形の消滅
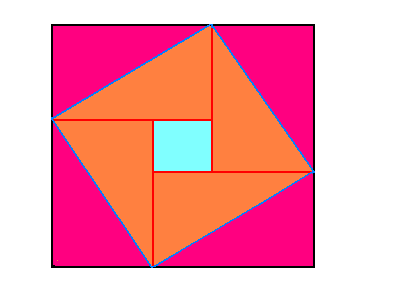
対角線で囲まれた部分のうち、中央の正方 形は、b = 0から出発するにしたがって、縮 小し、a = b時に消滅します
図１４ 円筒円錐図とピタゴラス定理拡張図 の比較 この現象を代数的にまとめようと、当初、 三角形rabの鋭角θをもとに、三角関数をく んでじたばたしたりしましたが、うまくいき ませんでした がしかし 以下の結論にまとまりました
図１６ 円錐 この円錐の立体の曲面のグラフを、任意の 平面で交曲線として切り取ったとき、その断 面の曲線を円錐曲線といい、二次曲線であり ます 筆者は、これが天体の力学にとって重要な 曲線だということで、高校時代にその数学的 な概念をしらべてみたことがあります その一部の試行では、数学の担当教科の教 諭に御世話になったのは今となっては懐かし い思い出です（郷愁が美しいのは、恥ずかし いことや挫折の悔しさを乗り越えたりわすれ てしまっているからです。 ♪真ん中は、道に迷っているばかり） ・双曲線と円 この円錐は、上項のカバリエリの原理の項 参照の、 頂点を原点に、 x軸を回転中心とする 頂点角度９０度＝π/2ラジアンの 円錐です
図１７ 円錐と円と双曲線 この円錐とx軸と直角にまじわる平面との 交曲線は、円であり またxy平面自身でないxy平面と平行な平面 とまじわる交曲線は双曲線になります 代数で証明しますと ・解が円になる例 x = 1 という平面で連立方程式を解くと y^2 + z^2 = 1 となってこれは円になります ・解が双曲線 z = 1 という平面で解くと y^2 + 1 = x^2 つまり x^2 - y^2 = 1 となってこれは双曲線を示します そのほかの円錐曲線は方程式を求めるのに 少々代数上のテクニックが必要です 得られる曲線の性質を考えるとき、三次元 区間での任意の存在角度の曲線（xyやzxなど の中間項が存在します）では、曲線形状の性 質が代数的にわかりにくいので、 xy平面などの基本平面上 （この場合はたとえばz = 1などの条件で方 程式からzの文字が消失し、xy平面への投影 とみなせます） の曲線であることが理想です そのためには、円錐の方程式そのものを、 希望する基本平面に対して原点中心に回転さ せてから、基本平面の方程式で再評価（つま りはその平面に交わらせる）させる必要があ ります ・放物線
図１８ ４５度回転された円錐 円錐を４５度y軸を中心に回転させます 円錐自体が原点頂点角９０度なので、zx平 面からみて円錐の一双のコーンは第一と第三 象現にのみ存在することになります 図形方程式を任意の角度で回転変換させる 場合には、 その図形を「その角度の負値で」回転変換 させた新座標系で再記述すれば得られること になります ここで味噌 （白みそです。 赤みそのほうがたしかに味が濃くて認識の 上ではわかりやすいですが、白のほうが、繊 細で味わいに奥行きがあって世界が深いです ただ、味覚がやわらかくデリケートなので、 なれないとその微妙な性質に気が付きません その味覚を愛することは個人の自由だとは 想いますが、こういう味覚がわからないなん て、野暮だねと笑うような京都の悪い面には かならずしも尊敬を払う必要はありません 検非違使に荘園の本貫を取り上げられてし まえば、伝統にはプライドしかもたれるよす ががないのでしょう 信長が足利将軍家におもっていた感情も、 こんなものだったかもしれません 寝かせて熟成させるという方向性は素材の 新鮮さを尊ぶもの：ファーストフード・スシ とは数直線上でおそらく符号が逆であり、 また実は優劣はつけがたいものです） 味噌（続き、笑）は、座標系そのものの回 転変換は、点を回転させる回転変換の概念と しての逆に相当し、変換行列は逆行列になり ます 点の変換は以下ですが、 |X|=|cos -sin||x| |Z| |sin cos||z| 座標系の変換には以下の行列を用います |x|=| cos sin||X| |z| |-sin cos||Z| この小文字の項を元方程式 に代入すればいいわけです θ= 45 とおき _ |x|=/2| 1 1||X| | | --| || | |z| 2 |-1 1||Z| ですからこれを代入して y^2 = x^2 - z^2 2y^2 = X^2 + Z^2 + 2XZ -X^2 - Z^2 + 2XZ = 4XZ を得ます 新座標系を旧表記に書き換え、 X -> x Z -> z y^2 = 2xz ですから xy平面と平行な平面との交曲線はたとえば z = 1とおき y^2 = 2x となりこれは放物線、 おなじく yz平面と平行な平面との交曲線は x = 1とおき同様に y^2 = 2z これも放物線になります なお、図中には表記しませんでしたが y = 1 とおくとこれは 1 = 2xz ですので双曲線を示します
図１９ 二つの放物線 ・楕円 上項の単純な円を楕円の一種とうそぶいて、 面倒な証明から逃げてもいいのでしょうが、 ここでは楕円らしい証明を示したいと考えま した
図２０ 楕円のための６０度回転された円錐 ここでは、さらに円錐を少し回転させ、６ ０度＝1/3 πラジアンを回転角として使いま す この場合、xz平面からみて、第二象現にま で円錐がはみ出してきます
図２１ 楕円幾何拡大 ：tan15の幾何の解説と数値 この円錐と xy平面と平行な平面z = 1との 交曲線は想定される楕円ですが その楕円のグラフの左の端 （x軸において負値の側） のx軸上の原点からの長さの値は、 図より tan15（３６０度単位） であると予測できます これは代数的には得られる楕円の方程式が、 y = 0の条件で x = -tan15の値 を解のひとつとして持てばいいわけです 帰納的証明ではありませんが、検証になり ます そのためにはtan15の具体的な値を知る必 要があります tangentの定義により sinθ tanθ = ------- cosθ です また 15度の三角関数の数値はあまり知られてい ませんので、角30度のcosとsinの数値から半 角の公式で値を求めます 二倍角の公式から半角の公式をみちびき、 cos 2θ = cos^2 θ - sin^2 θ = 2cos^2 θ - 1 または = 1 - 2sin^2 θ このペアはそれぞれ cos 2θ + 1 = +2cos^2 θ cos 2θ - 1 = -2sin^2 θ 1+cos 2θ ----------- = cos^2 θ 2 1-cos 2θ ----------- = sin^2 θ 2 ゆえに二乗のままtangentとして再定義し て 1-cos 2θ tan^2 θ = ---------- 1+cos 2θ ここで当然、 θ = 15 2θ = 30 ですから _ cos30 = /3 /2 であり tan^2 15 = _ _ 2-/3 (2-/3)^2 ---_ = -------- 2+/3 4-3 平方根をとって、 _ tan 15 = 2 - /3 を得ます 楕円３：円錐式の６０度回転変換 元となる方程式を y^2 + z^2 = x^2 とします 回転変換の行列は４５ ＝ π/2のときと同様 に |X|=| cos-60 -sin-60||x| |Z| | sin-60 cos-60||z| |x|=| cos60 sin60||X| |z| |-sin60 cos60||Z| _ 1| 1 /3||X| = -| _ || | 2|-/3 1||Z| ですからこれを代入します 準備として元の式を処理しやすいように変 形し、 y^2 + z^2 = x^2 y^2 = x^2 - z^2 4y^2 = 4x^2- 4z^2 としてからxとzを代入、 _ = X^2 +3Z^2 +2/3*XZ _ -3X^2 - Z^2 +2/3*XZ _ = -2X^2 +2Z^2 +4/3*XZ 係数２を通分、 _ 2y^2 = -X^2 + Z^2 +2/3*XZ 座標系をもとにもどし X -> x Z -> z _ 2y^2 + x^2 - 2/3*xz - z^2 = 0 として円錐の式を得ます 楕円４：平面との解曲線 xy平面と平行な平面z = 1 との交曲線をもとめると、 _ 2y^2 + x^2-2/3*x+3 -1-3 = 0 _ 2y^2 + (x-/3)^2 = 4 となります y二乗項、x二乗項ともに 係数はともに正値で なおかつ係数の値はひとしくないので、 代数の定義により、円ではなく楕円、 （図では俯瞰になりますのでうまく表現でき ませんでしたが、この楕円はy軸方向に縦長 に伸びた楕円です） またx軸との交点（解）は y = 0 とおき _ x - /3 = +-2 、 よって _ x = +-2 +/3 この一方の数値は、この項目の当初の 数値マイナスtan15と一致します 楕円編、証明終わり。 ２−３球の積分と円の積分の違い 球の積分は円の積分と根本的に異なるよう です 円弧の積分を代数的に考えますと、 |1 _____ | /1-x^2 dx |0 でありつまり |1 = | (1-x^2)^(1/2) dx |0 です これは初等的な方法では解くことができま せん 高校履修の範囲でははじめに私たちは置換 積分法を使用することを考えるものですが かんたんな置換積分法では次に述べる性質 を必要条件として要求します t = ax + b つまり微分して定数係数になることが必要 なので、中間変数ははじめの変数xの一次式 であることを要求します (ここでは特殊な関数のことは除外します) dy/dx = a このことは普通に考えると特殊な関数でな いかぎり、置換積分法でとける形式は以下の それであることになります | |f(ax+b) dx | この場合、中間変数tを以下の一次式で置 換するとき t = ax + b ですから | dt |f(t)*--- dt | dx と表現できます このような複雑な構成のように見えるそれ ですがこれは代数文法のトリックでdt/dx部 分は係数aとして左辺冒頭にくくりだすこと ができます | a*|f(t) dt | これらの数式はもちろん解くのは簡単です がしかし 円積分問題における次のような置換セグメ ントによる式は簡単に解くことができません t = 1 - x^2 このときはもちろんdt/dx項は定数にはな りません これは実は方法としては置換積分で解くこ とができますが、それは多分円周率や三角関 数の超越数的な性質と関連しているので、一 般教養としては解けないと考えてもかまわな いと想います 高校教科書の写しですが、この証明は項目 第４章に記載しておりますので興味があれば ごらんください しかし平方根の項目がそのまま残る円と違 って、 球体の体積を求める問題の時には この平方根：1/2乗部分 が微小体積の2乗部分と 相殺現象を起こしますので代数的には解く ことについての困難はありません また第３章で述べますが、球の表面積を求 める問題もこの平方根と自乗の相殺が起こり、 問題がごく簡単になります これは多分不思議なことでしょう これは、微細部分の円盤の微小体積・微小 表面積がすでに円弧としての性質を超越数π が具現化しているので、それ以上の積分的累 積演算に論理的複雑さがすくないからだ、と ポエジーとしては記述できるかもしれません ３球の表面積について 球の表面積を求める試行においては別種の 積分法の理解ができなくてはなりません これは二次元空間における曲線の長さを求 める試行と関連します これは球を回転体とみなし、回転体の表面 積をもとめる概念が必要だからです 回転体の体積を式としてもとめることによ って球：半球の体積をもとめた前の章の試行 と推論の進め方としては同じものです しかし回転体の表面積に関しては概念がや や複雑です
図２３ 球の例：後の項で説明 回転体の表面積 回転体の表面積の例においては、それは円 錐表面の微細成分の積算になりますので、概 念の把握がやや困難です (ただ、一度概念を把握してしまえば、球の 例、においては代数的な処理は比較的簡単に 進みます 逆にいえば、体積においても表面積におい ても球が持つ代数的な条件は、たいていは一 般的な回転体の方程式が満たすことができな い条件をいともあっさり飲み込んでクリアし てしまうがゆえに、 球とは代数体としても特殊な存在であると いえるかとおもいます) 曲線の長さを求める積分的概念は、円錐の 微細部分の表面積を求めるために必要ですが ここにもピタゴラスの定理が顔を出します ３−１回転体の表面積を求めるための考察 区分求積法としての概念の整理 回転体の表面積を求めるためには積分され る微細区間内の図形の幾何について把握され なければならないのはほかの積分問題とおな じです ふつう最初の積分問題として履修するxy平 面におけるx軸と関数曲線でかこまれた領域 を求める問題が、 微細長方形矩形の積算であることを思い起 こしてください 回転体の体積においてはこの矩形がハムの ようなスライス円盤（たまご２個に対してハ ム３枚が適当です）の微細体積に該当したた め 定積分表記で y = f(x)のとき |β V = 2π| f^2 (x) dx |α と表現することができました 復習ですが xy平面における円を r^2 = x^2 + y^2 としたとき、 y = f(x) ならば f^2(x) = y^2 ですから |+r V = 2π| r^2 - x^2 dx |-r が球の体積になり、これは比較的簡単に解け て先だっての 4 - *πr^2 3 になります よく言えばエレガント悪く言えば格好つけ の回答は上記のようになるとおもいます 回転体の表面積を求める問題は
図２５ 微細円筒で近似 この考え方だと、曲線上の任意の点 P（xp,yp）においてスライスされたハムの赤 い表面のリングの面積、あるいは愛犬の黄色 いコーンのリングの面積、 Δr * 2π*yp 幅 円周の長さ の成分としての積算を考えれば回転体の表面 積が求められることになります
図２６ 曲線の回転積分：体積表面積共通 代数的に別の言い方で言えば、曲線の長さ をその各点における半径y (つまりypの一般 形)として三次元空間に回転したものが、そ の求めるべき回転体の表面積であるわけです つまり、：定積分表記 |β 2π| Δr *y dx |α と一般的に書くことができます ３−２曲線の長さを求める積分について 曲線の長さをもとめる場合は、代数形式 では普通の微小長方形矩形の面積積算とは 異なる演算を行います
図２７ 微小三角形の屋根の長さをΔrとおいて いますから dxの幅によって規定される微細領域にお いて以下の関係があり Δr^2 = dx^2 + dy^2 ：ここではΔとdを同義にしています これはピタゴラスの定理そのものです 曲線の線分の長さは、定積分のある区間に おけるこのΔrの総和です（区間を一般化す ればもちろん不定積分になります） これを数式で表現すると以下のようになり ます （重要：普通の積分問題でよく見かける項目 dxはあくまで矩形面積積算の共通項としてく くられている形式であります つまりx軸と曲線に囲まれた定積分面積を 構成する微細矩形面積Δsは、 Δs = y*dxであり、 | | |Δs =| y dx | | またy=f(x)であれば | = |f(x)dx | と表記されているに過ぎません そのため長さの積分では当初の共通項とし てはで出てきません） | |Δr | | ___________ = |(/Δx^2+Δy^2) | みなれた項目dxが存在していない理由は、 dxが微小矩形面積積算の共通項だからです 今回積算するものは微小三角形の斜辺の長 さであり これはdxとしての共通項をくくりだしませ ん。しかし代数的な処理によって同じような 形式に変換することができます （これで代数的に積分ができます） ここで Δx -> dx Δy -> dy とし また dx^2/dx^2 をつかってdx項をくくりだすと | ___________ | / dy | / 1+ (----)^2 dx | / dx | となってみなれた積分形式に変換できます これが任意の曲線y=f(x)の長さをもとめる 一般式です（かならずしもこの式が一般的に 解けるものではありません） 同様に、任意の曲線y=f(x)の回転体の表面 積を求める一般式は上項の式が積分記号内部 ではΔrに相当しますから | ______________ 2π| y * / 1 + (dy/dx)^2 dx | と示すことができます ３−３曲線関数としての円弧の長さを求める ・そのためにつまり円を微分し導関数を得る ３−２項において、代数的には回転体の表面 積を求めるためにはその基となる曲線関数の長 さをその基となる曲線関数の長さを意味する関 数が積分として得られていなければならないこ とが分かりました つまり代数的に球の表面積を求めるためには、 その基となる曲線図形として円弧関数の微分す なわち導関数が、得られていなければなりませ ん 円弧を微分します つまり次の問題を解くことになります dy d -- = --(r^2 - x^2)^(1/2) dx dx ここで合成関数の微分法則と dy dy du -- = -- * -- dx du dx 拡張整関数の微分法則を用い、 d -- x^n dx = n*x^(-1 + n) を使います u = r^2 - x^2 とし 与式 = d d -- u^(1/2) * -- (r^2 - x^2) du dx = (1/2)u^(-1/2) * (-2x) -x = ------- u^(1/2) -x = -------- _______ /r^2-x^2 となります ３−４円弧の微細屋根長さΔrをもとめる dy/dxを二乗し１を加えて平方根にすれば よいのですから ここでもちろん dy^2 x^2 ---- = ------- dx^2 r^2-x^2 ゆえに dy^2 r^2 1 + ----- = ------- dx^2 r^2-x^2 根号とdxをつけると _________ / dy^2 / 1 + ---- dx = / dx^2 r -------- dx = Δr _______ /r^2-x^2 です この式は次項で重要です これでΔrが得られました ３−５円弧の回転積分として半球の表面積 を得る 積分される微細項を代数的に整理します ここで _______ y = /r^2-x^2 でありますから y * Δr = ________ / dy^2 ________ r y * /1 + ---- dx = /r^2-x^2 -------- dx / dx^2 _______ /r^2-x^2 = r * dx (初めて演算したときに、おもわず「何で！」 と叫んでしまいました) よって与えられた式は |r | |r 2π|r dx = 2π*r| x | |0 | |0 2π*r*r = 2πr^2 これは半球なので 4πr^2 となります ３−２−１付記微細円筒近似の傍検証 直線を回転体とすると円錐になりますが、 この意味で母曲線を直線とし、回転体として の円錐の表面積をもとめ、 初等古典的な円錐の表面積とつき合わせて みます 円錐の表面積を求める古典的な式は後の項 で解説しますが、ここでは式のみを表記しま す 最も簡単な円錐として直線y = xがx軸の周 りに回転できる円錐を考えます 円錐の表面積は π*斜面の稜線の長さ＊底面円の半径 で求めることができます このばあい、稜線は２の平方根、 底面円の半径は１ですから、この円錐の表 面積は _ /2π です 積分式でも解いてみます y = xですから dy/dx = 1 よって表面積は定積分表記で | 2π| yΔr dx = | y = x より |1 ___ _ |x^2|1 2π| x/1+1 dx = 2/2π|---| |0 | 2 |0 よって _ /2π で一致します 問題なのは、母曲線の形状ではなくて微細 円錐を円筒に近似するいわば誤差の議論なの でこの場合の円錐の表面積を微細円筒で近似 することで正しく求められればこの代数的手 段が正しいであろうと推測できます（証明で はありません） ３−６円錐微細部分による近似 結果から言えば、円錐を円筒で近似しても かまわないことは、以下述べる代数整理の結 果からはわかったようです(ようです、とい うのは自分は専門家ではないので、以下の論 理の進め方に間違いがある可能性があるから です) ３−７円錐の表面積：直接には式未使用 円錐の表面積は立体図とその展開図から 初等的にもとめることができます
図２８ 円錐とその展開図 底面円の半径をr１、 七夕の飾りを作るように、円錐に切込みを 入れて展開図にした場合の半径をr2とおくと、 展開図の円の面積を底面円の円周を分子と する分数比で面積を縮小すればいいわけです から 2πr1 πr2^2 * ----- 2πr2 = πr1 * r2 となります ３−８備考：微分における円弧の性質 ：直交する、接線と半径としての法線 ああでもないこうでもないと幾何図を書い ていて、偶然に気が付いたことですが、 微分法に関して、円弧は特殊な性質をもっ ていることに気が付きました
図２９ 円とその接線 円弧上の任意の点をP(xp,yp)とおくと、 原点Oからの線分OPは、点Pにおける接線 と直角に交わることが円の性質からわかりま す つまり半径でもあるOPは接線に対する法線 でもあるわけです これを代数的に表記すると y dy -- * -- = -1 x dx という微分方程式になります これは代数的に整理でき、 dy -x -- = -- dx y となりここで _________ y = /r^2 - x^2 ですから dy -x -- = -------- dx _______ /r^2-x^2 となります 以前の項でもとめた円弧関数の導関数と一 致します。あたりまえといえばあたりまえな のでしょうが。 ３−９円錐の縦断面三角形としての円弧の 接線とx軸との交点から円錐斜面の辺半径を 求める
図３０ 接線と交点 ここで円弧上の任意の点Pにおける接線と x軸の交点を考えます
図３１ その接線の回転と母円錐 この接線をx軸周りに回転させてできる円 錐が表面積を近似する微細円管を含む円錐で す 円錐の底面円は、点Pを含む定義で考えま す また曲線の長さの微細成分Δrは、点 Pを基点として考えます 接線の方程式は一般に y - yp = ｆ'(xp)(x - xp) でありますから 円弧の微分の定義により dy -x -- = -- dx y よって -xp y - yp = ---(x - xp) yp ゆえに：y側符号変換 yp(yp - y) = xp(x - xp) ここでx軸との交点でありますからy = 0 よって yp^2 = xp(x - xp) r^2 - xp^2 = xp*x - xp^2 r^2 = xp*x r^2 x = ----- xp ここでこの円錐の高さに相当する長さhは点P のx成分を単純に減じて r^2 h = -xp + ---- xp この円錐の縦断面の三角形の斜辺の長さをrｔ とおくと ピタゴラスの定理により rt^2 = h^2 + yp^2 = r^2 (xp + -----)^2 + (r^2 - xp^2) xp r^4 xp^2 + ------ - 2r^2 + r^2-xp^2 xp^2 r^4 ---- - r^2 xp^2 r^2-xp^2 r^2--------- xp^2 ゆえに rt = r ________ yp --/r^2-xp^2 = r---- xp xp 想わぬ単純な形式にあれ、と想いました 筆算時には気がつきませんでしたが、円 錐の断面三角形（図３０では黄色）は単位 円に関する三角関数三角形（図では白、辺 の名前で言えばr,xp,ypで構成される三角 形）と相似であるので、実は、当然でした。 正確には白と黄色の合体と、白が相似で あることにより対応正比例が上記の式と対 応します ともかく、これでrｔが得られました ３−１０微細円錐面積成分としての近似式の作成 ：この方法での表面積の算出 円錐の展開図で考えます
図３２ 接点近傍近似円錐部分の展開
図３３ 円錐幾何を平面に近似展開する試行１ 点Pを含む円錐展開図の 最外周の長さは、2πypであり、 外周から母曲線の微細長さΔr分だけの幅 分レコード状に内側に位置する円周の長さは、 Δr減分だけ正比例で減少するため、 Δr 1- ---- rt だけ最外周より小さくなります この比率をSrI：SurRoundingInnerとしま す（下着の腰周りではありません） これと最外周と囲まれたたまねぎリングの 一世代層の微細面積は、 円の面積をもとめたときに概念としてもち いられた「ぎざぎざ切り分け法」を応用して 細長いリボン状の長方形へと変形することを 考えます このたまねぎのリング一世代分を台形状の みじんに切り分け、内周と外周とを互い違い にならべると短辺と長辺がうちけしあって、 見かけ上長方形に近い形になります 直感的には、これを幅と長短辺の平均から なる長方形としてすぐ面積を出したい誘惑に かられますが 微積分に関しては影にすぐ無限大がひそみ ますのでやや慎重さが必要です ただ、厳密に代数を追うのではなく、ここ では相同図形でなりたつことを確認するにと どめます これは円の外周の一部の円環の面積に関す る問題ですから、一般的に円の面積において 成り立てば良いことになります 円の面積は「πかける半径の二乗」で あらわさられる公式で示されますが、 これは古典的概念的にはこの「ぎざぎざ法」 が有名でしょう
図３４ 円錐幾何を平面に近似展開する試行２ ぎざぎざ法は別項付記扱いにします ここではこのぎざぎざ法がなりたつとして 話を進めます 以下の記述が厳密であるかはわかりません 微細円錐の面積Δsは 最外周の長さ + 一段階内側の内周の長さ Δs = 幅 * ------------------------------------ 2 となります ここで 内周の長さ = 最外周の長さ * SrI ですから 1 Δs = 幅 * 最外周の長さ * -(1+SrI) 2 ここで 1 Δr Δr ---(1+1 - ---) = 1+ --- 2 rt 2rt であり r 幅 = Δr = --dx yp 最外周の長さ = 2π * yp 円錐斜辺の長さ:rt yp rt = ---*r xp よっておきかえて、 r*dx r*dx xp Δs = ----- * 2π*yp * (1 + ----*-----) yp yp 2yp*r xp = 2πr*dx * (1+ -----*dx) 2yp^2 |r |r xp = 2πr| dx + πr| ------dx dx |0 |0 yp^2 後ろの項に dx が二回あるので 0 にな ることが期待できますから そのときは半球の表面積として値 2π*r^2 を得ます これは半球ですから全球としては 4π*r^2 です また一般に | x |------- dx |r^2-x^2 が積分できるかどうかについては代数的に 試行としては可能です 部分分数をとり x a b ------- = --- + --- r^2-x^2 r-x r+x とすると分子と分母を干渉させて恒等式に でき ar +ax + br -bx = 0 +x | | V V a+b=0 a-b=1 V V b = -a > 2a=1 よってa=1/2 行列表記で、 1 (a,b) = - (+1,-1) 2 となります。よって 2 * 与式 = |-1 | 1 |--- dx + |--- dx |r+x |r-x 置換積分によって（式の下段は係数の解説） = -log r+x - log r-x ネイティブの- r-x由来の- 与式 = -log r^2-x^2 ------------- 2 これは円弧ですからすくなくとも xの範囲は0からrのあいだ、 その意味では値は有限値であり、 一方項の中にふたつめのdxがありますので、 これは極限で0、その意味でこの項は0になる ことが期待できます ３−１１「円の面積を求めるためのぎざぎ ざ法」
図３５ 円の分割 n=8
図３６ 円の分割と近似 n=8 筆者はこれをはじめてみたときは小学生で した これは厳密には長方形の面積ではなく平行 四辺形の面積です 直感としてこの極限図形が長方形に近づく ようにみえますが、その仮定が正しいのであ れば、その面積は確かに円周率＊半径の二乗 です 良い機会ですので、高等数学でこの極限値 が確かに長方形に近づくことを証明してみた いと想います 証明を簡単にするために半径を１とします 円を任意の自然数nで分割することを考え ます このレモンケーキのかたちに分割された円 の断片で最外周の円弧としての皮を考えのな かから除外し、二等辺三角形だけを考えます 二等辺三角形は二つの直角三角形に分割で き、その直角三角形の鋭角は、当然二等辺三 角形の鋭角の半分です 弧度法で表現すれば、その角度は全周の2n 分の1ですからおのおのの直角三角形の面積 は 2π/2n = π/nですから cos π/n ＊sin π/n ------------------- 2 また直角三角形は二等辺三角形の倍の数あ りますから2n個、よって総面積は n * cos π/n * sin π/n という近似式になります これのn -> ∞における極限の値がわかれ ばいいわけです θ = π/n と便宜的におくと = n * cosθ * sinθ n = --- * sin 2θ 2 = n 2π --- * sin--- 2 n しかしn が限りなく大きくなるとき、この 式は∞/0 形式の不定形となってしまいます これを関数の微分係数：導関数とみなして x 2π = -- * sin--- 2 x と考え、極限値だけが問題なのですからロ ピタルの定理により（筆者はロピタルの定理 自体の証明を知りません） lim g(x) lim g'(x) ------ = ------ x->h f(x) x->h f'(x) より、 sin2π/x ------- 2/x を考えます 準備、複合合成関数の微分として分子部分 のsinをとらえ dy dy du -- = -- * -- dx du dx u = 2π/x とおき d 1 -- x^(-1) = - --- = t dx x^2 とおくと du -- = 2π * t dx d --sin 2π/x dx +cos 2π/x *2πt ----------- = ---------------- d 2 2t -- -- dx x = π * cos 2π/x ここで n=x -> ∞のとき 与式 ＝ πとなります 証明の途中で、この円が任意の半径rをも つことを加味したければ、二乗扱いの項とし て係数扱いで外部にくくりだされますが、そ の代数は割愛します これで、円の面積は、一辺が半径、もう一 辺が半径の円周率倍の長さをもつ長方形に変 換できます ４ピタゴラス派の秘密主義と時代背景 ：円弧の積分と超越数的性質 ピタゴラスはばかではありません、が。 べつのファイルのreadmeに「受験競争がな いからこそ学院は学問のおもしろさ奥深さを もっと紹介するべきだ」というようなことを 書いたようなおぼろげな記憶があります （ただ、それはおしえる側の話だけではなく、 学ぶ側も分かったような気持ちで自分をごま かすのではなく知識欲の「飢え」でどんどん 噛み付いていくことが必要なのかもしれませ ん） これはしかし確かに教える側がその面白さ を十二分に実践経験で知っている必要があり ますが そのようなくだりで 「ピタゴラスの馬鹿」 という一語を書いてしまったこととがあり ます。そのことについて。 各自氏がしらべてもらえば歴史上の有名人 でもありますので、ピタゴラスがどのような 生涯をおくったかはすぐ出てくると想います 日にちと書名は失念してしまいましたが、 最近：年末年始２０１２では新聞の書評欄に もでていました 自分の記憶のもっとも古い部分では、ある アメリカのテレビ番組で 「彼の一派が、神秘主義者であるといわれた ゆえんです」とのくだりでした 当時の自分は、遠隔ロボットがもたらす画 像にくぎ付けになっていて、 そのような西洋根源歴史に対する関心は当 時の自分にはありませんでしたが。 新興国であるアメリカは自分たちの文化の ルーツというものに対して慢性的なかつえが あるもののようです 連邦の建物がしばしば旧世界の伝統を模し た様式：でも鉄筋：なのはそういう理由があ るのでしょう ピタゴラスは、自分の記憶がまちがってい なければ、都市ポリス政治の後期か末期、ソ クラテスやプラトンの時代の人だと記憶して います ローマの黎明期のアルキメデスよりは昔の 人ではあるようでした アルキメデスは思索の結果現在で言えば積 分法：数式は別にして、考え方の意味では微 分よりも積分のほうが理解しやすい：の原型 となる考え方にもいたったそうでありますか ら 少なくともアルキメデスの中では、無限小 や無限積算を介して実際的な意味での無限と いう概念に対するアレルギーはなかったよう です どちらかといえばアルキメデスはプラクテ ィカルな性格だったのかもしれません 業績も工学系の分野に傾いているようで、 これは水道橋を含め、ローマカルタゴ時代が、 密室思索に傾きがちだったギリシア特にアテ ネの時代の、反省でもある当時の世界の風潮 だったからなのかもしれません その意味ではアルキメデスは、アリストテ レスやイスケンデル・ズルカルナインの系譜 に連なるといってもいいかもしれません イスケンデルとは地名としてギリシアのア ルカディアをも連想させますが、これは実は サラセン世界にとっても、聖なる響きを持つ のでした ピタゴラスはこのような時代のひとつ昔、 事実上ギリシア都市国家時代が終焉する前後 の人でした 当時のキーワードを列挙すると、 ペリクレス クレイステレス オストラキスモス デマゴーグ デロス同盟 デロリンマン 筆者は世界史は赤点でした。苦い記憶です。 ピタゴラスの処世は、ピタゴラスの定理に 関する態度に現れていると想います
図３７ 正方形とその対角線 正方形の対角点を結ぶ斜辺の長さが、正方 形の一辺を単位として _ /2=1.141421356...... である無限「非循環」小数であることを発 見してしまったとき、魔方陣でもあるその正 方形から当時のギリシア世界では到底認める ことのできない邪悪でおそろしいドラゴンが 召還されてしまったのでした ひえー ピタゴラスの一派は逃げ惑い、丘を焼き尽 くしたかのドラゴンの存在とその召還の呪文 を決して一門以外には口外しないことを堅く 示し合わせたのでした これが、ピタゴラスの一派が秘密主義者で あるとされた逸話です 実際かれらは開かれた議論集団というより は、教団の色彩が濃く、ややドグマチックで、 この系譜が多分欧州の修道院の系譜につなが っていくのでしょう なぜ無限非循環小数が思索世界のなかでは 脅威なのかというとたとえば 0.1212121212...... という無限であるけれどもしかし循環する 小数は、 0.12 0.0012 0.000012 0.00000012 ........ の総和として定義でき、 これは ∞ Σ 12*10^(-2n) n=1 と定義できます これはその性質として、数の構造を把握で きます しかし一般に平方根はこのような数式によ る定義ができません ですから これは2の平方根だよという記号 _ /2 を使用して紙の上に宣言するしかないのです このことが、論理が自分たちの集団でいわ ば存在意義の保証であったあろうかれらが、 自分たちの権威と安全保障をおびやかすもの に 平方根をはじめとする無理数：無限非循環 の小数：を脅威とみなしたのも想像できます 保守的な教師の態度そのものにみえるのは 私だけでしょうか まあ、当初の現実はそんなところだったで しょう 数の神秘と神聖さを言うのであれば、すで に分数を発見したとき、もしそれが特定の個 人による発明であれば「神聖な数を分割した」 というかどで、ブルーノよろしく火刑にかけ られたかもしれません ここにはなんとなく守りの態度がある、と 軍事国家マケドニアの王子なら言ったかもし れません プラトンの系譜がどの程度コスモポリタン の精神によっていたかはいまでは知るべくも ないかもしれませんが、すくなくとも開かれ た世界が理想であるという態度から かれらのような保守的な態度はいわば腐敗 したアテネの既得権益というりんごにすくう、 つつくと奥に引っ込むちいさな虫としていじ められたことはあったかもしれません 過剰な思索や密室はしばしば肉体や暴力に 敗北します ゼノンのパラドックスが現実世界では問題 にならないように、フィジカルな体操や肉体 が実は、直感的には時空が実はプランク単位 あたりで不連続でじつはデジタル的な量子遷 移に支配されていることを教えてくれるよう に、 運動不足というものはやや思考や態度に悪 い影響を与えるもののようです 意思、というものはべつにニュルンベルグ で振り回すべきものじゃなくて 十分に近いグラフの曲線間同士で、いわば グラフ格子のくりこみてきな量子的荒さによ って状態がジャンプすることを指します その意味では、神経細胞が、粗い網目でつ ながり、なおかつシュヴァン細胞のスフィン ゴリン脂質でとびとびに電気絶縁されている ことは、恣意という意味での意思を意識が操 作するためには必要なことのようです 意思や行動が物理学的に現象として可能で あるためには、空間構造や神経構造が、物性 的に密でなおかつ高度に微分的に連続である ことは、かえってよくないことなのかもしれ ません 最近の計算機科学の発達により、仮想空間 で人工連想の実験ができるようになったそう ですがそのレポートによると、完全に均一な 系よりも、多少構造的に荒さがある系のほう が、人間や動物の意識に似た反応を返すこと が多いようです 遠い未来では、おそらく機械が思考をする ことも可能になるかもしれません ただ、それがユートピアであるとは限らな いことは自明のことでしょうが ピタゴラス教団の態度を批判することを最 新のトピックで書け、といわれたら、こんな ような文章になるかもしれません マケドニアの王子の気分から言えば、神秘 主義派、とは「うしろむきの腎虚のじじい」、 という暴言になるのかもしれません 論理帰納にしか過ぎませんが、イスラムで はその意味で開放的で実際的な気分のあるア ルキメデスのほうがピタゴラスよりも人気が あるのかもしれません 過酷な環境では、まず人間が生きていかな ければならないので、思索の腐敗というギリ シア末期の負の面よりも、まず実際的な体系 のほうが尊重されたであろうことは、容易に 想像できます その意味では、イスラム教徒にとって、ピ タゴラスの態度は海峡をはさんだビザンツの 大聖堂にみえたかもしれません ただ、コンスタンチンノープルへの弁護で はないですが、開放的で行動的なプラトンの 系譜が、結果、広大な領土を得た結果として の奢侈と堕落と言う意味でのローマ帝国の外 交政治暴力になった気配を指摘することはし なければならないかもしれません （ローマとサラセンとは、異邦人をあまり差 別しなかったという意味で根幹の一部はおな じだと想います。） スペース・オペラの例を引くまでもなく、 アメリカ人は自分の国をローマ帝国の栄光に なぞらえることを好むようです 搾取される辺境や属州、ネロやカリギュラ の名前をとりあえず忘れても、史実はともか く世界を開いた英雄アレキサンダーを嫌いな アメリカ人はそういないとおもいます すくなくとも思想的実際的なベトナムの挫 折まではそうだったでしょう 素朴な善意としての「正義の輸出」という 気分は、裏の思惑はともかくとして、いわゆ る宇宙開発が大衆にうけいれられたことと たぶん共通していることなのでしょう 「宇宙戦隊」とはみな正義の味方であり、脚 本が屈折してくるのは、ベトナム以降、イン ナートリップという逃避でもあるドラッグ文 化の時代と一致しています くしくも、第二次世界大戦からアメリカは 工業国家となりましたから、より開放的で実 際的なアルキメデスを支持したがる気分がた とえばその時代にもあったのかもしれません しかし古代ではローマ期に至り、バルカン 半島ではピタゴラス学派的な教条主義が勢力 を伸ばし、これがビザンチンに至るギリシア 正教の系譜へとつながっていくのかもしれま せん そういう気分から言えば、ギリシア的神秘 主義とは、パックスロマーナの開かれた理想 からいえばあまり気持ちの良いものではなか ったのかもしれません のちにコンスタンチンノープルを陥落させ たのは、イスケンデルの文化輸出の恩恵を受 けたオスマントルコでした 無理数やそれに連なるピタゴラスの定理は たしかに不思議なものですが、それを内側に 隠匿してしまう傾向に、おそらく思想として のピタゴラスの不幸があったのかもしれませ ん 実はピタゴラスの定理とはそもそも「円」 という最悪最恐の数学概念の定義でもありま すから、そこからはおそろしいほどの神秘が ぞろぞろとでてくることは、ガウスやライプ ニッツの研究で明らかになったことでした ピタゴラスの定理は r^2 = a^2 + b^2 ですが、 これは 1 = cos^2 θ + sin^2 θ でもあります 三角関数の恐ろしさは、みかけではわかり ません。 小兵が勝利を総なめにするようなものです たとえば、円の面積をもとめる問題は、積 分の文法で書くと以下のようになります |r | (r^2-x^2)^(1/2) dx |0 あるいはr = １として |1 | (1-x^2)^(1/2) dx |0 これは、簡単には解けません。 すくなくとも単純な置換積分法では代数的 に解くことができません この数式があらわしているのは半径rの任 意の円の四分割ですから、 π*r^2 /4 であるはずです しかし、円周率πは超越数であり、無理数 です 有限回の定義では定義することができない のでこれは収束する無限級数の和としてのみ 求めることができます 積分としての与式には、すくなくとも初等 的には無限級数として展開できる項目はみあ たらないように想えます このあたりの知識は自分は知りませんが、 大学で習うテイラー展開あたりの概念が必要 で、数学としては１８世紀の研究を待たなく てはならないようです 古代のドラゴンは、ライプチヒあたりに出 現したようですね この意味で三角関数は無限級数の和として 表現できますが、この式はxを置換積分とし て三角関数に変換して初めて解くことができ ます 以下は高校教科書の意訳ですが x = sinθとおくと、 1 -x^2 = cos^2θ また dx -- = cosθ dθ よって置換積分により 与式= |π/2:1=sin α then α=π/2 | cos θcos θdθ |0 積分は積よりも和あるいは一次式の 置換積分の方が解きやすいので、 cos^2 θを二倍角の公式で和に変更する cos^2 θ - sin^2 θ = cos 2θ ========== -1+cos^2 θ = 2cos^2 θ -1 = cos 2θ 1+cos 2θ cos^2 θ = --------- 2 をもちい 与式 = 1|π/2 1|π/2 -| dθ + -| cos 2θ dθ 2|0 2|0 | <-----------------> V η=2θ とおいて置換積分 1| |π/2 dη -|θ| ---- = 2 2| |0 dθ | 1|π=2*/2 dη V -| cos η *--- dη 2|0 =2*0 dθ π/4 | V | |π | -sin η | | |0 | V -0+0=0 よって値はπ/4 代数的な直接証明ではありませんが、 これは次のように考えることもできます
図３８ 変数をθとする場合の円の積分 以下の図形でθを０に近づける場合を考えます 図形Aの面積は π/4-θ 図形Bの面積は 直角三角形ですから sinθcosθ sin 2θ --------- = ------ 2 4 θ->0とし ABの和はπ/4になります ＊ 一方、一度円の円周と面積がもとめられて しまえば、球体の体積と表面積がつるりと安 産のようにもとめられてしまうことはおそら く老荘の陰門の神秘に似ていることなのかも しれません 女体の神秘はたしかに不思議ですが、それ はどこにでもある万民のものであり、一部の 教条主義者が独占できるわけのものではない ことは一般的にも自明のことです 思想に正誤はあるものではありませんが、 閉鎖的な態度は場合によっては賢明なもの ではないのかもしれません 一般論、脳（ここでは人間における言語と いうデジタル）と遺伝子は人間の少なくとも ここ数十万年の歴史では、助け合ってきた面 もありますが、反面その優位性に関して覇権 をあらそってきた面があります これはそのまま、男性と女性、父性と母性 との質的な相克でもあるのでしょう 意味の上において多少複素平面上の原点回 転のずれの気味がありますが. ただ、男性性と女性性というものは観念に 過ぎず、とる座標系によって見方が変わる相 対的なものです RNAワールドでもあったサイトゾル原形質 の立場からみれば、実は遺伝子もそれは脳と ともに「お経のような西方」であり、アナロ グではなくデジタルなものです 言語の元となった有髄神経が実は拡散ホル モン的な原始神経細胞を脂質による電気絶縁 でより０と１的なデジタル処理系の性質を大 きく添加したように、 DNAもまた半酵素物質であるRNAの電気的絶 縁的安定化修飾進化：DNAはRNAの一部脱水に よって、より「石油的」になり、酵素的な仕 事から遠ざかりまた：石油的な安定化から情 報保存と伝達の仕事に専念するようになった ことによって、 おそらく３０数億年前の「バクテリアの脳」 としてはじまったのでした この世界においては、遺伝子が男性、原形 質が女性的要素として分類されるでしょう 遺伝子が利己的に見えるのもあたりまえか もしれません 笑 ただ、遺伝子もまた原形質：つまり細胞質 の中にもある物理学としての宇宙の性質：を おおいに利用しているという意味では もし遺伝子を男性として見立てるとすると、 宇宙の女性的な原理の大きなお世話になって 自分の中にある遺伝情報を発現していること は大きな事実です 具体的にいうと、遺伝子はたとえば生体内 のすべての情報をまるで電子スキャナーによ る空間的なビットマップとして記憶している のではありません もしそんなことをしたら、遺伝子の情報量 はその個体あたり現状の爆発倍もの容量の数 値が必要になるでしょう トピックとしてIPS細胞培養のようなレポ ートにも時々現れていますが、たとえば異種 の細胞をシャーレの中で混合培養した場合に、 自然と生体組織あるいは臓器の組織配列を髣 髴とさせる構造に育ってくることはよくある ことです 出来上がってきたものの複雑さからは想定 しかねるかもしれませんが、 最も簡単な腔腸動物で、細胞の種類は３種 類、人間でさえもおそらく５０種類ぐらいし かないでしょう（厳密には基準の取り方にも よります） 人間の遺伝子では、おそらくこの数十種の 細胞のあり方を記述するコードしかおそらく 乗っていません その意味では、細胞同士の話し合い、連絡 と協調の実際は、おそらく遺伝子の上ではわ るくいえば行き当たりばったりの進化の歴史 による数値の調整のようなものにすぎないの でしょう 数学的な言い方をいえば、細胞の遺伝子に 乗っている情報というものは数列の漸化式的 な情報でしかありません 協調安定した個体に収束するか、破綻に爆 発するかは、単に数値とその適応による宇宙 空間でもある個体あるいは細胞内の環境の結 果でもある自然現象の効果でしかありません 遺伝子は、自然現象の宇宙空間を利用する ことによって 「認識」を上手に手抜きをしているのです われわれは、代数的に超越数を理解するこ とはできませんが、しかし直感的に円という 概念を把握できるのはこのようなことを眺め たあとでは、自分たちが有機的な肉体に座し ているからこその帰結であることを、認識す ることができるのだと想います また女性は子宮で考えるからこそ、怒らせ ると超越数のドラゴンよろしく恐ろしいもの かもしれませんね 男性女性というトピックでいうと、フェニ ミズムの流行からでしょうか、女性性や母性 を無条件に持ち上げる風潮が続きましたが、 別に異常でも狂気でもなく、たとえば西太后 もまた女性性の発現であることは臨床的には 重要なことです：「太々」 まんがの女の子がかわいくこずるく振舞う のと、バーゲンでおばさんが「もっとないの」 とずうずうしく迫ってくるのは、実はおなじ ものです 「むかしはあんなにかわいかったのに」 ソクラテスは恐妻家だったそうで。 ＊ 意外に知られていませんが、経済文明史的 には厳密には「ギリシャ文明」という言い方 は間違いです ギリシャは食料経済の意味ではエジプトの 穀倉穀物に依存しており、そこ経済は陶土： 補遺a参照：ブドウ（ワイン）オリーブの交 易でした 食料自給率を別にして、実はギリシャはい わば縄文段階経済と言い換えてもよく、 その意味ではギリシャは石器時代とおなじ 意味においてアシュール文化とおなじ意味で のギリシャ「文化」と言い換えた方がいいか もしれません 文明とは、狭い意味では王権による穀倉の 統治による余剰食料の備蓄を担保として、通 貨概念が発行され、農業以外の二次産業が発 生する形態を指します この意味では、もちろんギリシャはオリエ ント地域において文明の主体ではなく、その 全体構造の一部にしか過ぎませんでした 棟梁産業が重要なものであることはいまも むかしもかわりませんがしかし、自分で食料 を生産できない蒲田や東大阪やそしてたぶん 横浜が、「文明」をなのることには無理があ ります 元町にあるものは、文化であって文明では ありません：補遺b参照 このような地域では、統治のための王権が 必要ではありませんから、むしろ情報重視の ために自由がたっとばれ、また同時に同属的 意識からなる差別的意識も希薄でした アルカディアが理想の意味を持つ言葉であ るのは、それが比較的縄文的な世界観に近い からです ただこれは、ギリシャにおいては古代の頃 の話で、次第に時代が下るにつれ、事態はよ り変質していったようです 筆者の記憶にあやまりがなければ、 ネフェルテティはギリシャ系だったようで すし、プトレマイオス王朝はギリシャ系を先 祖にもつとされています つまりエジプト本土とギリシャの結びつき が強固になればなるほど、アフリカ大陸のよ くいえば伝統的、わるくいえば保守的な要素 がながれこんできたことは歴史の必然として、 おそらくあったでしょう このことがアテネの腐敗や、エーゲ海の政 治文化の独自性を消滅させることをまねいた ことは、潮流的に原因として、あったかもし れません このようなことが、あるいは象徴として、 ピタゴラス学派がアカデミアというよりは教 団色がつよい傾向があることを時代的事象と して示しているような気がしてなりません 以後も、地中海世界はクレオパトラやイシ ス信仰などエジプト的な呪縛にずっととらえ られ続けるのです 人間の弱さに対して、数千年の伝統という ものはかくも圧倒的なものなのでしょうか ただ、腐敗に終わった古代ギリシャに対す る弁護ではありませんが、 農耕文明というものはどうしても保守的政 治的には鈍重な傾向がありますから、域外の 行動も発想も剽悍なひとびとから干渉、支配 をうける傾向があります 衝突があれば反応があるのが物理学でもあ る政治ばけがくですから 遊牧民や縄文段階民族の支配を農耕地域が うけることは多かったでしょう ただ、軍略が男性的な攻撃である反面、い わば「土の毒」で征服者を腐敗させるのはい わば、女の復讐であるわけなのです、って、 クレオパトラですねこれは。 ピタゴラスが必死に隠した、無理数にまつ わる数学的なドラゴンは、悪い意味でもある ルネッサンス期（正確にはその後期）にヨー ロッパでもう一度目覚めることになります 個人的には、これを数学における１９世紀 の悪夢とよんでいます １９世紀に編み出された概念のほとんどが、 難解すぎて自分には理解できないからです 日本では、関が原の戦いが１６００年ちょ うど、江戸開府がすくしおくれて１６０３年 です 江戸時代は二世紀半続きました 江戸の花は家光公元禄と家斎公の文化文政 のふたつ、を考えると、わかりやすいです 元禄と文化文政のあいだに、悪名高い天保 大飢饉がおきましたが、この１８世紀（１７ ００年代）は、科学雑誌によると太陽活動な んとか極小期で、地球の平均気温がごくわず かその前後に比して低くなったそうで、全世 界的な穀物の不作をもたらし、ヨーロッパで はその生活苦がフランス革命とそれにつづく 欧州の政治的名混乱をひきおこしました 仏革命は、１７００年代後半、 その後の混乱の象徴であるナポレオンは、 １８００年代前半の人です マザーグースに、子供をおどかすのに 「寝ない子のところにはボナパルトがくるぞ」 というのがあるそうですが 筆者がオンライン辞典で確認したところで は、 ラグランジュは仏革命でラボアジエが殺さ れたことをずっと気にしていて、 またナポレオンの周りの交友には若干の数 学者があったようです（信じられないことで すが、ナポレオンの活躍は、実は長崎経由で ほとんど同時代に江戸時代の日本に伝わって いました 保守・蘭学どちらの勢力も、世界情勢が実 はとんでもない時代であることは、知ってい る人は知っていたようです） オイラーやガウスは、革命以前の人ですね ベルヌーイやハミルトンはこの１８００年 代のひとです ナポレオンの知己の数学者にフーリエ（フ ーシェ）と言う人がいました。 フーリエ変換のフーリエです 彼は公職に在ったとき、シャンポリオンと いう少年にナポレオンがエジプト遠征のとき にもちかえった（筆者の記憶違いかもしれま せん）考古物を見せたのがきっかけで、この 少年がのちにエジプト象形文字の解読（ロゼ ッタ・ストーン）をすることになったことを、 筆者は大昔前述の番組でみたことがあります ：補遺c参照 １９世紀の当時は、エジプト的なピタゴラ スがひた隠しにしてきた秩序を破壊する数学 上の無限というばけものが数式のうえであば れまわっている最中でした 「そして、ふりだしにもどる。」 結果と原因がクラインの壷のように、ぐる ぐるもとにもどるめまいを感じます。 miyama. ーーーーーーーーーーーーーーーーーーーー 補遺a 陶土 良質の陶土とは、粒がそろっていてなおか つ成分ができるだけ純粋な石英長石質のもの が最良とされていますが、これはたいていの ばあい、風にふるいにかけられた安山岩質の 火山灰です。熊本のシラス台地の土です ギリシャ地域は、紅海地裂谷からくる黒鉱 グリンタフ火山活動 （キプロスの銅はおそらく黒鉱でしょう。エ ーゲ海自体は地列谷ではないのかもしれませ んが、この狭い地域に大地を左右に引き裂く 力がかかっているのかもしれないなと自分は ギリシャ地域の左右に良く似た地図の上の海 岸線を眺めながら想っていたものです このような地域では地殻応力の地震による 断層は土地沈降の正断層として働き、地震の 後には地盤沈下をもたらします どのくらい沈降したのかは知りませんが、 アトランティスは地震によって浸水したので しょう このような構図は実は日本列島日本海側の 地質と相同性があり、日本海はかつて陸だっ た地域が海底の拡大によって海になった地域 です 小陸塊の衝突により部分的に日本の陸地に なったところでは、かつて平賀源内や宮沢賢 治が興味をしめした山形岩手国境の硫化物鉱 床があります 和同開珎の銅とキプロスの銅は地質学的に はおなじものです 日本海の沖には、かつて陸地だったところ がおそらく正断層沈降で海中に没した「大和 堆」という台地があり、これはアトランティ スの地質学的な運命に相当します この正断層性沈降は日本海地域の西南日本 列島に広範囲に働いているらしく、 琵琶湖や瀬戸内海は、かつて陸地だったと ころに複数の断層群ができて沈降し、水や海 水が侵攻してできた地形です この仮説が正しいかどうかはわかりません が、もしそうならば瀬戸内海はエーゲ海であ り、福原明国貿易の平氏一門はギリシア・フ ェニキア人であることになります あとの項で述べますが、交易に依存する経 済は厳密な意味では文化であって文明ではあ りません その意味では、土地本位制農業文明である 源氏勢力に、平家の文化が駆逐されてしまう のはたしかに歴史の上では時間の問題であっ たのかもしれません） であり、イタリア地域は、アフリカプレート がヨーロッパに沈み込む地域なので、富士・ 箱根型火山灰大爆発型火山：ベスビオ、エト ナの活動が活発で、 この両者とも火山地域です 悲劇だったポンペイ、かつて文書のよみま ちがいで大西洋にあると誤解されたアトラン ティスであるクレタの悲劇は地質がもたらし たものです 余談ですが、わが富士山も、むこう数十万 年のうちには山体の半分以上が、爆塵となっ て吹っ飛ぶ噴火を起こすかもしれません 補遺b 文明と封建 ・文明 文明というものは、実はおもっくるしいも のです 前項のことがらを重要な前提とするならば、 広義の統治のために必要な広義の税が必要で す ある国家の、必ずしも良いことばかりでは ない「文明度」というのを統計的に計りたい のであれば、統治機構の発達の度合いと、領 民がどれだけの税的負担をになっているのか ということに着目すべきでしょう かならずしもテクノロジーの発達の度合い は尺度にはなりません その意味で、あらゆる文明とは、腐敗と圧 制の誘惑の隣に住むことになります すべての文明の基本は、備蓄食料の量とい う担保が基本ですが、耕作可能な農地という ものも無限に開墾増殖が可能なものではあり ません その意味では、すべての文明の基本はゼロ サム経済であり、（制度や王朝の陳腐化リス クという意味での）経年腐敗やしばしば弱者 が犠牲になる間引きがついてまわるものです 逆にいえば、文明とは農村であり、伝統的 に理由も無く本家が分家を足蹴にするもので あり、また支配が制度的なものである以上、 いよいよ支配が破綻する場合は、住民や領民 の大半が殺害される場合もそんなにめずらし いことではありません このことは、近代でも本質的にはかわりが なく、植民地支配（理由なき先取占有）や大 戦争もその力学の流れにあるものです 古代でも近代でも最大の税とは兵役でした テクノロジーの一種に医療がありますが、 一種の皮肉として、はやりやまいで早くして 死んでいたはずの子供が、進歩した医療のお かげで、今度は戦場の消耗品として死ななけ ればならなくなった、というものがあります ざっとの素読で申し訳ありませんが、軍医 であった鴎外はこのような種類のことをずっ と考えていたようです 漱石と鴎外は、立場上あいいれなかったは ずだ、という指摘をどこかで読んだ記憶があ りますが、たしかに胃弱な漱石氏は、重病に くるしむ娘を安楽死させようとはおもわなか ったでしょう これは故遠藤周作氏が描いたかもしれない テーマかもしれませんが、たとえば 「せんせい、そこにあるのは毒薬だろ、おね がいだからそれを俺に打ってくれよ、 もしなおったら、また戦場で人間を殺さな ければならない、 そんなのは、いやだ」 薄い本なら一冊分の戯曲にあたります 「高瀬舟」に通じるところがあるかもしれま せん ・封建 では文明でなければいいのか、というとこ れは人の世の常、反面そういうものばかりで ありません 文明でない、ということは制度や法律がは っきりしていないということでもありますか ら 慣例や人情でものがきまるということでし た 余談ですが、江戸時代があんなにながくつ ずいたのは、幕藩体制の厳しさの反面、その ような粘液質の安全弁がよく機能していた面 があります ただ制度や法律がはっきりしていないとい うことは君主の暴走や危機がおこったとき、 迅速に効果的に物事に対処できないというこ とを意味します その意味では、我々の意識はうわべはとも かく江戸時代を引きずっているもののようで その意味では、おそらく日本人は原則的には 原子炉を運転すべきではないのかもしれませ ん（その体質が変わらない以上、むしろその 良い点を引き出す努力をすべきかもしれませ ん） ヨーロッパの封建制でも事情はおなじだっ たらしく、暴走する狂った君主が領民を虐殺 した記録は、トランシルバニア以外にもかな りにもかなりあるようです・・・封建制には 狂気の君主をとめる手段がありません 地方分権と封建制は内実ではおなじもので すが、予算上幕府連邦の権力を制限すると、 独立自治体が内部地方の荒廃や人権弾圧を江 戸表がさばけなくなります（これは主張では なくて現象記述です） 内政不干渉とは、建前上公儀隠密とはやみ にほうむられても文句は言えない存在である ということですから、「なにかあっても当局 は一切感知しないのでそのつもりで」という 言葉が実によく象徴しています ただ、筆者はどちらの仕組みのほうがより 良いという主張をするものではありません どちらも一長一短があります たとえば日本が歴史上これからどちらの方 に転がるのか、それはどちらの制度のほうが、 負担効率として無理がないのか、ということ が現象として決めることでしょう 別に我々は職業政治家自身ではありません。 この土地が、ふたたび国家であることをあき らめる（江戸体制は全体として国家ではあり ません）のであってもわれわれは生きていか なければならないのですから ヨーロッパ封建制度では、その様な君主の 暴走をとめるのは江戸幕府に変わる権力は教 皇権でした ただ、教皇権というものは悪い意味での 「お上の威光」に過ぎない面があり、バチカ ン自身は強大な軍事力をもっていたわけでは ありません（幕府自身の軍資金は、三代家光 の頃に、ほぼからになっていました） 幕府や教皇権は鎌倉幕府のように、恥をか き、みかぎられたらそれでおしまいで、精神 的な権威があればこそ直接的には主従関係の ない雄藩が長州征伐にもしたがってくれるの です そういう意味では、かならずしも峠のむこ うの勢力がお家騒動を助けてくれるわけでは なく、暴走する馬鹿殿から身を守るすべは、 国境の内側では、実力しかないわけです（阿 部一族） 規制緩和と地方分権はいっけん響きがあま いですが、そのじつ、だれもたすけてくれな いと言う意味で実力と体力を鍛えるしかない ということでもあります （規制緩和とは、世の中を一強百弱にして、 その一強から法人税を期待する、ということ であり 以下はゼロサムに近い社会での企画企業論 になりますが ：人間の考えることには統計的な意味でそう 大きな違いはなく、 ：つまりわかりやすく受けるようなアイデア は逆に差別化が難しく、また独自的なものは 収支の上では認知軌道にのるまでに数十年が かかるり、 これは実は新しいアイデアというものは実 際にはおなじ需要を満たしている業者業界が すでに存在しているからで、暴力：アヘン効 果による甘言顧客破壊を含む：による世代交 代に訴えない限りは、その交代に１、２世代 かかるということでもあります つまり利益が出るのは二代目あるいは二番 手からということになるからです スチーブンソンによる鉄道機関車の発明か ら実際の鉄道の普及に時間がかかったことが 象徴的です その意味で、証券とは本来一株最低５０年 ＝１．５世代：は保持しなくては原則的に意 味がないことになります またドリームはしばしば憶測が甘いもので すからゼロサムに近い条件では、たいていの ベンチャーの９０パーセントは破綻し ：これはけっして高い数値ではありません、 直接的な比較はできないかもしれませんが 生命の進化の歴史ではppmのレベルの子孫が 次の世代を引き継いだりします その関係者は年齢が低い場合はつぶしのき かない失業者になります。彼らを劣悪な賃金 で雇うのが、残った一パーセントである「一 強」であり、 中国の王朝の群雄割拠の終息期の力学にそ れはしばしば現れています：規制緩和＝無頼 実力主義 この場合、政府は形式上漢帝ですが実質的 な支配者は火星で酸素を牛耳る曹操になるわ けです） 補遺c 東方名 ちなみに、「シャンポリオン」という苗字 はいささか響きに東方の味があると感じるの はわたしだけでしょうか。 イオン、アポロン、エンディミュオン。 ：ここでのイオンはaeonではなくてionです 笑 欧州では地続きなこともあり、東方系のひ とびとがおおく流れ着いてきています おそらくありそうなことは、学校に東方系 の少年がいて、かれが先祖のいた地域の事物 に興味を持っていたがために、フーシェ氏が その子にそういう話をした、という要素もあ ったかもしれません たとえば、欧州で「パシャ」という姓がと きどきありますが、この名前は源平藤橘よろ しく、トルコの名門の名前なのです ーーーーーーーーーーーーーーーーーーーー